题目内容
11．
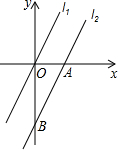如图，在平面直角坐标系中，直线l1对应的函数表达式为y=2x，直线l2与x轴、y轴分别交于点A，B，且l1∥l2，OA=2，则线段OB的长为（ ）| A． | 3 | B． | 4 | C． | 2$\sqrt{2}$ | D． | 2 |
分析 先写出A点坐标，则利用两直线平行的问题，设直线l2对应的函数表达式为y=2x+b，再把A点坐标代入求出b的值，则可确定B点坐标，于是可得到OB的长．
解答 解：∵OA=2，
∴A（2，0），
∵l1∥l2，直线l1对应的函数表达式为y=2x，
∴直线l2对应的函数表达式可设为y=2x+b，
把A（2，0）代入得4+b=0，解得b=-4，
∴直线l2对应的函数表达式为y=2x-4，
∴B（0，-4），
∴OB=4，
故选：B．
点评 本题考查了两直线相交或平行问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解；若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同．
练习册系列答案
相关题目
2．“端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
（2）列式计算说明，如果顾客在“端午节”当天购买该种粽子超过200元，那么到哪家超市花费更少？
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
| x （单位：元） | 实际在甲超市的花费 （单位：元） | 实际在乙超市的花费 （单位：元） |
| 0＜x≤200 | x | x |
| 200＜x≤300 | 10+0.95x | x |
| x＞300 | 10+0.95x | 30+0.9x |
阅读：
6．平面直角坐标系中，三条直线l1：y=ax，l2：y=x-a，l3：y=a（a≠0）的公共点是（ ）
| A． | （-1，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，-1） | C． | （$\frac{1}{2}$，1） | D． | （1，$\frac{1}{2}$） |
如图，在?ABCD中，CH⊥AD于点H，CH与BD的交点为E，如果∠1=70°，∠ABC=3∠2，那么∠ADC=60°．
19．若a+b=-6，ab=6，则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值为（ ）
| A． | $\sqrt{6}$ | B． | -$\sqrt{6}$ | C． | 2$\sqrt{3}$ | D． | -2$\sqrt{3}$ |
