题目内容
3.为了解某市参加中考的40073名学生的身高情况,抽查了其中1000名学生的身高进行统计分析.下面叙述正确的是( )| A. | 40073名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 本次调查是全面调查 | |
| D. | 1000名学生的身高是总体的一个样本 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:A、40073名学生的身高情况是总体,故A不符合题意;
B、每个学生的身高是个体,故B不符合题意;
C、抽查了其中1000名学生的身高是抽样调查,故C不符合题意;
D、1000名学生的身高进是总体的一个样本,故D符合题意;
故选:D.
点评 考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.

练习册系列答案
相关题目
14.若y=kx+b中,当x=-1时,y=1;当x=2时,y=-2,则k与b为( )
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
18.一个多边形的内角和是720°,这个多边形的边数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是( )
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
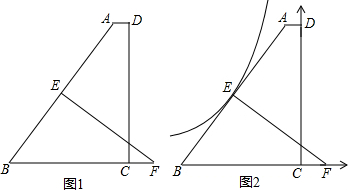
12. 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )| A. | a | B. | 2a | C. | $\frac{3}{2}$a | D. | $\frac{5}{2}$a |
13.若点A(-5,y1),B(1,y2),C(2,y3)在反比例函数y=$\frac{-{a}^{2}-1}{x}$(a为常数)的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
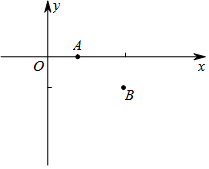 如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).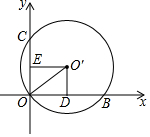 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )
如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )