题目内容
1. 如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE.
如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE.
分析 连接AO,根据等腰直角三角形的性质可得AO=CO,∠CAO=45°,∠ACB=45°,再求出∠OAD=∠OCE=135°,根据同角的余角相等求出∠AOD=∠COE,然后利用“角边角”证明△AOD和△COE全等,根据全等三角形对应边相等证明即可.
解答  证明:如图,连接AO,
证明:如图,连接AO,
∵△ABC中,∠BAC=90°,AB=AC,
∴AO=CO,∠CAO=45°,∠ACB=45°,
∴∠OAD=∠OCE=135°,
∵OD⊥OE,
∴∠COD+∠COE=90°,
又∵∠AOC=90°,
∴∠AOD+∠COD=90°,
∴∠AOD=∠COE,
在△AOD和△COE中,$\left\{\begin{array}{l}{∠OAD=∠OCE}\\{AO=CO}\\{∠AOD=∠COE}\end{array}\right.$,
∴△AOD≌△COE(ASA),
∴OD=OE.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
7.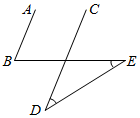 如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=35,则∠B的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
8.要使(x2+ax+1)(-6x3)的展开式中不含x4项,则a应等于( )
| A. | 6 | B. | -1 | C. | $\frac{1}{6}$ | D. | 0 |
5.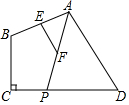 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )| A. | 线段EF的长先减小后增大 | B. | 线段EF的长不变 | ||
| C. | 线段EF的长逐渐增大 | D. | 线段EF的长逐渐减小 |
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )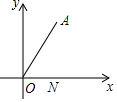 如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.
如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.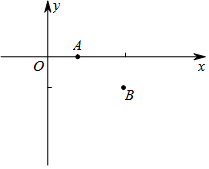 如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).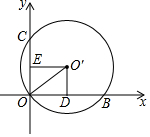 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )
如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )