题目内容
16．
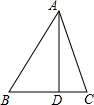如图，△ABC中，AD⊥BC于D，若AB=15，AC=13，BC=14，求AD．
分析 设BD=x，则CD=14-x，根据勾股定理得出方程，解方程求出x的值，再由勾股定理即可求出AD的长．
解答 解：设BD=x，则CD=14-x，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵△ADB与△ACD均为直角三角形，
∴AD2=AB2-BD2=AC2-CD2，
即152-x2=132-（14-x）2，
解得x=9，
∴BD=9，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12．
点评 本题考查了勾股定理；熟练掌握勾股定理，由勾股定理得出方程求出BD是解决问题的关键．
练习册系列答案
期末集结号系列答案
相关题目
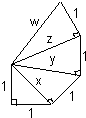x=$\sqrt{2}$，y=$\sqrt{3}$，z=2，w=$\sqrt{5}$．
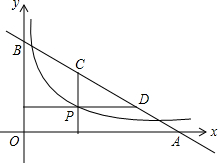如图，P是函数y=$\frac{\sqrt{3}}{x}$（x＞0）图象上的一点，直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A，B两点，过P作x轴、y轴的垂线与该直线分别交于C，D两点，则AD•BC=4．
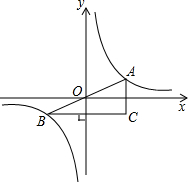如图，A、B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点，AC平行于y轴，BC平行于x轴．
6．下列计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | 2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$ | C． | $\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$ | D． | 5$\sqrt{\frac{1}{5}}$=1 |