题目内容
6.下列计算正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$ | D. | 5$\sqrt{\frac{1}{5}}$=1 |
分析 根据二次根式加减乘除混合运算法则对各个选项进行计算,即可判断.
解答 解:$\sqrt{2}$+$\sqrt{3}$不能合并,A错误;
2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$,B正确;
$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$(a≥0,b≥0),C错误;
5$\sqrt{\frac{1}{5}}$=$\sqrt{5}$,D错误,
故选:B.
点评 本题考查的是二次根式的性质和混合运算,掌握二次根式加减乘除混合运算法则是解题的关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$ | B. | $\sqrt{(-9)×(-25)}=\sqrt{9}×\sqrt{-25}=(-3)×(-5)=15$ | ||
| C. | -3$\sqrt{\frac{2}{3}}$=$\sqrt{{{(-3)}^2}×\frac{2}{3}}$=6 | D. | $\sqrt{{{13}^2}-{{12}^2}}=\sqrt{(13+12)(13-12)}$=5 |
14.抛物线y=2x2+4x+3的图象与x轴有( )
| A. | 一个交点 | B. | 两个交点 | C. | 没有交点 | D. | 无法确定 |
1.下列四个点中,在函数y=-$\frac{2}{x}$图象上的点是( )
| A. | (-1,2) | B. | (-0.5,1) | C. | (-1,-2) | D. | (2,1) |
11.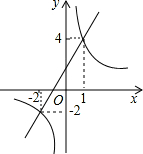 一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}(m≠0)$,在同一直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )
一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}(m≠0)$,在同一直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )
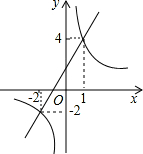 一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}(m≠0)$,在同一直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )
一次函数y1=kx+b(k≠0)与反比例函数y2=$\frac{m}{x}(m≠0)$,在同一直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )| A. | -2<x<0或x>1 | B. | x>1 | C. | x<-2或0<x<1 | D. | -2<x<1 |
18.若$\frac{a}{3}$+1与$\frac{2a+1}{3}$的绝对值相等,则a的值为( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | 2或$\frac{4}{3}$ | D. | 2或-$\frac{4}{3}$ |
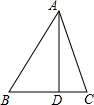 如图,△ABC中,AD⊥BC于D,若AB=15,AC=13,BC=14,求AD.
如图,△ABC中,AD⊥BC于D,若AB=15,AC=13,BC=14,求AD.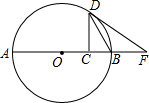 如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.
如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.