题目内容
19. 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=$\frac{3}{2}$,BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E.设AP=x,DE=y.求y关于x的函数关系式,并指出自变量x的取值范围.
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=$\frac{3}{2}$,BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E.设AP=x,DE=y.求y关于x的函数关系式,并指出自变量x的取值范围.
分析 由AD∥BC得出∠DAE=∠APB,结合两个直角得出△ADE∽△PAB,由相似三角形的性质即可得出y与x之间的关系,由P是BC边上的一个动点(点P与点B不重合)可得出x的取值范围.
解答 解:连接AC,如图,
由勾股定理可得AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\frac{5}{2}$,
∵P是BC边上的一个动点(点P与点B不重合),
∴AB≤AP<AC,即$\frac{3}{2}$≤x<$\frac{5}{2}$.
∵AD∥BC,
∴∠DAE=∠APB(两直线平行,内错角相等),
又∵∠ABP=∠DEA=90°,
∴△ADE∽△PAB,
∴$\frac{DE}{AB}$=$\frac{AD}{AP}$,即$\frac{y}{\frac{3}{2}}$=$\frac{1}{x}$,
∴y关于x的函数关系式:y=$\frac{3}{2x}$($\frac{3}{2}$≤x<$\frac{5}{2}$).
点评 本题考查了动点问题的函数图象、相似三角形的判定以及性质,解题的关键是找出△ADE∽△PAB,依据相似三角形的性质即可得出y与x之间的关系.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
8.已知函数y=$\frac{k}{x}$(k≠0)的图象过点(a,b),则它必经过的另一点是( )
| A. | (a,-b) | B. | (-a,b) | C. | (-b,a) | D. | (b,a) |
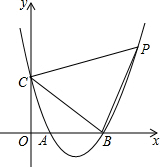 如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标.
如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从A开始沿折线AC→CB→BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒$\frac{4}{3}$个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P与直线l同时停止运动.当点P在BA边上运动时,作点P关于直线EF的对称点,记为点Q,若形成的四边形PEQF为菱形,则t=$\frac{6}{5}$或$\frac{30}{7}$.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从A开始沿折线AC→CB→BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒$\frac{4}{3}$个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P与直线l同时停止运动.当点P在BA边上运动时,作点P关于直线EF的对称点,记为点Q,若形成的四边形PEQF为菱形,则t=$\frac{6}{5}$或$\frac{30}{7}$.

 已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.
已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC. 如图所示,已知△ABC中AD,BE分别是BC,AC的高,且BD=AD.求证:
如图所示,已知△ABC中AD,BE分别是BC,AC的高,且BD=AD.求证: