Question

1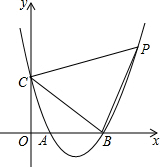．如图，抛物线y=x²-4x+3与坐标轴交于A，B，C三点，点P为对称轴右侧的抛物线上一点，若tan∠PCB=2，求P点坐标．

Answer 1

分析 根据题意首先得出直线BC的解析式，进而利用PR的长结合tan∠PCB=2得出P点横坐标，进而求出答案．

解答 解：过P作PQ⊥X轴于Q，交CB延长线于R，过P作PH⊥BC于H，
设P（m，m²-4m+3），
∵抛物线y=x²-4x+3与坐标轴交于A，B，C三点，
∴x=0，则y=3；
y=0，则0=x²-4x+3，
解得：x₁=1，x₂=3，
故A（1，0），B（3，0），C（0，3），
设直线BC的解析式为：y=kx+b，
则$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$，
故直线BC解析式：y=-x+3，
∴R（m，-m+3），PR=m²-4m+3-（-m+3）=m²-3m，
∵OB=OC=3，∴∠CBQ=135°，∴∠HPR=45°，
∵CO=OB，
∴∠OCR=45°，
∴CR=$\sqrt{2}$OQ=$\sqrt{2}$m，
∴PH=RH=PR÷$\sqrt{2}$=$\frac{\sqrt{2}}{2}$m（m-3），
又CR=$\sqrt{2}$OQ=$\sqrt{2}$m，
∴CH=$\sqrt{2}$m-$\frac{\sqrt{2}}{2}$m（m-3）
=-$\frac{\sqrt{2}}{2}$m（m-5）
由tan∠PCB=$\frac{PH}{CH}$=-$\frac{m-3}{m-5}$=2，
解得：m=$\frac{13}{3}$，
则m²-4m+3=$\frac{40}{9}$，
故P（$\frac{13}{3}$，$\frac{40}{9}$）．

点评 此题主要考查了抛物线与x轴的交点，正确结合锐角三角函数关系得出P点横坐标是解题关键．