题目内容
设n,k为正整数,A1=
,A2=
,A3=
…Ak=
,已知A100=2005,则n=( )
| (n+3)(n-1)+4 |
| (n+5)A1+4 |
| (n+7)A2+4 |
| (n+2k+1)Ak-1+4 |
| A、1806 | B、2005 |
| C、3612 | D、4011 |
考点:无理方程,规律型:数字的变化类
专题:规律型
分析:利用多项式的乘法把各被开方数进行计算,然后求出A1、A2、A3,的值,从而找出规律并写出规律表达式,再把k=100代入进行计算即可求解.
解答:解:∵(n+3)(n-1)+4=n2+2n-3+4=n2+2n+1=(n+1)2,
∴A1=
=n+1,
(n+5)A1+4=(n+5)(n+1)+4=n2+6n+5+4=n2+6n+9=(n+3)2,
∴A2=
=n+3,
(n+7)A2+4=(n+7)(n+3)+4=n2+10n+21+4=n2+10n+25(n+5)2,
A3=
=n+5,
…
依此类推Ak=n+(2k-1),
∴A100=n+(2×100-1)=2005,
解得n=1806.
故选A.
∴A1=
| (n+1)2 |
(n+5)A1+4=(n+5)(n+1)+4=n2+6n+5+4=n2+6n+9=(n+3)2,
∴A2=
| (n+3)2 |
(n+7)A2+4=(n+7)(n+3)+4=n2+10n+21+4=n2+10n+25(n+5)2,
A3=
| (n+5)2 |
…
依此类推Ak=n+(2k-1),
∴A100=n+(2×100-1)=2005,
解得n=1806.
故选A.
点评:本题是对数字变化规律的考查,对被开方数整理,求出A1、A2、A3,从而找出规律写出规律的表达式是解题的关键.

练习册系列答案
相关题目
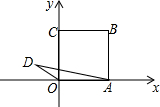 如图所示:OABC是正方形,OD∥AC.|AD|=|AC|,若|OA|=1,则D的坐标是( )
如图所示:OABC是正方形,OD∥AC.|AD|=|AC|,若|OA|=1,则D的坐标是( )A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
已知x3+y3-z3=96,xyz=4,x2+y2+z2-xy+xz+yz=12,则x+y-z=( )
| A、6 | B、7 | C、8 | D、9 |
用长度为2l的材料围成一个矩形场地,中间有2个隔墙,要使矩形的面积最大,则隔墙的长度为( )
A、
| ||
B、
| ||
C、
| ||
| D、l |
已知|x|=3x+1,则(64x2+48x+9)2005=( )
| A、0 | B、1 | C、-1 | D、无法计算 |