题目内容
6．
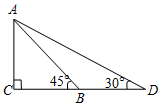如图，为安全起见，幼儿园打算加长滑梯AB，将其倾斜角由45°降至30°，已知滑梯AB的长为4m，点D，B，C在同一水平地面上，那么加长后的滑梯AD的长是$4\sqrt{2}$m．
分析 Rt△ABC中由AC=ABsinB求得AC的长，再根据Rt△ACD中∠D=30°可得AD=2AC，即可得出答案．
解答 解：在Rt△ABC中，∵sinB=$\frac{AC}{AB}$，
∴AC=ABsinB=4sin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$，
在Rt△ACD中，∵∠D=30°，
∴AD=2AC=4$\sqrt{2}$，
故答案为：4$\sqrt{2}$．
点评 本题主要考查解直角三角形的应用-坡度坡角问题，熟练掌握三角函数的定义是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠A=90，BD是角平分线，若AD=m，BC=n，则△BDC的面积为$\frac{1}{2}$mn．
14．在5张形状相同的卡片上，分别写有下列5个命题：
①同位角相等；
②三角形中至少有两个锐角；
③三角形三个外角的和是360°；
④三角形中至少有一个角大于60°；
⑤如果两条直线平行，那么同旁内角的平分线互相垂直．
从中任意抽取一张卡片，抽取到卡片写有真命题的概率是（ ）
①同位角相等；
②三角形中至少有两个锐角；
③三角形三个外角的和是360°；
④三角形中至少有一个角大于60°；
⑤如果两条直线平行，那么同旁内角的平分线互相垂直．
从中任意抽取一张卡片，抽取到卡片写有真命题的概率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
如图，在扇形AOB中，∠AOB=90°，$\widehat{AC}$=$\widehat{BC}$，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2$\sqrt{2}$时，则阴影部分的面积为2π-4．
11．若-72a2b3与10ax+1bx-y是同类项，则x、y的值为（ ）
| A． | $\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=-2\\ y=2\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$ |
如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．请说明理由．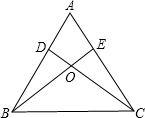
已知：如图，锐角三角形ABC的两条高BE、CD相交于点O，且OB=OC，