题目内容
18.如图1,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,动点E从点A出发自终点B运动,过点E作DE⊥AC交AC于点D,点A关于ED的对称点为点P,点P落在射线AC上,过点E作EF⊥BC交BC于点F,连接PE,PF;设AE=5x.(1)则DE=3x,AD=4x(用x的代数式表示);
(2)当x为何值时,△EFP是等腰三角形?
(3)如图2,当点E关于直线FP的对称点E'恰好落在射线AC上时,则$\frac{{S}_{△EPF}}{{S}_{△EPA}}$的值为$\frac{5}{8}$.(直接写出答案即可)

分析 (1)由勾股定理得出AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,证出DE∥BC,由平行线得出△ADE∽△ACB,得出$\frac{DE}{BC}=\frac{AD}{AC}=\frac{AE}{AB}$,即可得出答案;
(2)由对称的性质得出PD=AD=4x,证明四边形CDEF是矩形,得出EF=DC=4-4x,CF=DE=3x,分情况讨论:①当FP=FE=4-4x时,在Rt△PCF中,由勾股定理得出方程,解方程即可;
②当PE=PF时,PC=PD=4x,得出方程4-8x=4x,解方程即可;
③当EP=EF=4-4x时,在Rt△PDE中,求出EP=$\sqrt{(3x)^{2}+(4x)^{2}}$=5x,得出方程4-4x=5x,解方程即可;
(3)由得出的性质得出四边形EFE'P是菱形,得出EP=EF,由(2)③得:x=$\frac{4}{9}$,再由三角形面积公式即可得出答案.
解答 解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
∵DE⊥AC,∠ACB=90°,
∴DE∥BC,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}=\frac{AD}{AC}=\frac{AE}{AB}$,即$\frac{DE}{3}=\frac{AD}{4}$=$\frac{5x}{5}$=x,
∴DE=3x,AD=4x,
故答案为:3x,4x;
(2)∵点A关于ED的对称点为点P,
∴PD=AD=4x,
∵EF⊥BC,DE⊥AC,∠ACB=90°,
∴四边形CDEF是矩形,
∴EF=DC=4-4x,CF=DE=3x,
分情况讨论:
①当FP=FE=4-4x时,
在Rt△PCF中,由勾股定理得:(3x)2+(4-8x)2=(4-4x)2,
解得:x=$\frac{32}{57}$,或x=0(舍去),
∴x=$\frac{32}{57}$;
②当PE=PF时,PC=PD=4x,
又∵PC=4-8x,
∴4-8x=4x,
解得:x=$\frac{1}{3}$;
③当EP=EF=4-4x时,
在Rt△PDE中,EP=$\sqrt{(3x)^{2}+(4x)^{2}}$=5x,
∴4-4x=5x,
解得:x=$\frac{4}{9}$;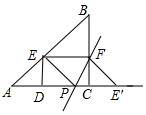
综上所述:当x为$\frac{32}{57}$或$\frac{1}{3}$或$\frac{4}{9}$时,△EFP是等腰三角形;
(3)当点E关于直线FP的对称点E'恰好落在射线AC上时,四边形EFE'P是菱形,如图所示:
∴EP=EF,由(2)③得:x=$\frac{4}{9}$,
∴$\frac{{S}_{△EPF}}{{S}_{△EPA}}$=$\frac{\frac{1}{2}(4-4x)•3x}{\frac{1}{2}•8x•3x}$=$\frac{4-4x}{8x}$=$\frac{1-x}{2x}$=$\frac{1-\frac{4}{9}}{2×\frac{4}{9}}$=$\frac{5}{8}$;
故答案为:$\frac{5}{8}$.
点评 本题是几何变换综合题目,考查了轴对称的性质、勾股定理、相似三角形的判定与性质、等腰三角形的性质、菱形的判定与性质、矩形的判定与性质等知识;本题综合性强,有一定难度.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 2x+2y=2xy | B. | (xy)2÷$\frac{1}{xy}$=(xy)3 | C. | (x2y3)2=x4y5 | D. | 2xy-3yx=xy |
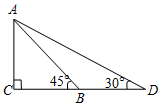 如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
 如图,在四边形ABCD中,点E在对角线AC上,AB∥DE,∠ACB=∠EDA,AB=EA,求证:AC=ED.
如图,在四边形ABCD中,点E在对角线AC上,AB∥DE,∠ACB=∠EDA,AB=EA,求证:AC=ED.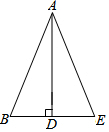 已知:如图,△ABE中,AD平分∠BAE,且AD⊥BE,垂足为D.
已知:如图,△ABE中,AD平分∠BAE,且AD⊥BE,垂足为D.