题目内容
1.探究规律:先阅读下列材料,再根据要求回答问题
42-12=3×5
52-22=3×7
62-32=3×9
…
根据上面规律填空
①202-172=3×37;20152-20122=3×4027;
②第n个等式可表示为(n+3)2-n2=3(2n+3).
分析 由题意可知:等号的左边是相差为3的两个数的平方差,右边是3乘这两个数的和,由此规律得出答案即可.
解答 解:①202-172=3×(20+17)=3×37;20152-20122=3×(2015+2012)=3×4027;
②第n个等式可表示为(n+3)2-n2=3(n+3+n)=3(2n+3).
故答案为:37,4027,(n+3)2-n2=3(2n+3).
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字的运算规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某商店的老板销售一种商品,要以不低于进价120%的价格出售,但为了获得更多利润,以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价( )元时,商店老板才会将商品卖给你.
| A. | 80 | B. | 100 | C. | 120 | D. | 160 |
9.计算:a2•(-a)3的结果正确的是( )
| A. | -a5 | B. | a5 | C. | -a6 | D. | a6 |
13.若点P(m,n)在第二象限,则点Q(m,-n)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.下列运算正确的是( )
| A. | $(3-2\sqrt{3})(3+2\sqrt{3})={3^2}$-2×3=3 | B. | $(2\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=2a-b$ | ||
| C. | ${(3-2\sqrt{3})^2}={3^2}-{(2\sqrt{3})^2}$=9-12=-3 | D. | $(\sqrt{a}+\sqrt{a-1})(\sqrt{a}-\sqrt{a-1})={(\sqrt{a})^2}-{(\sqrt{a-1})^2}$=a-(a-1)=1 |
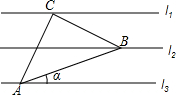 已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.
已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.