题目内容
4.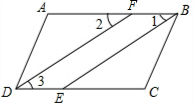 如图,∠ABC=∠ADC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.请说明∠A=∠C的理由.
如图,∠ABC=∠ADC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.请说明∠A=∠C的理由.解:因为BE、DF分别平分∠ABC、∠ADC(已知),
所以∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC(角平分线定义)
因为∠ABC=∠ADC(已知).
所以$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ADC(等式的性质)
(请完成以下说理过程)
分析 根据角平分线定义得出∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC,求出∠1=∠3,求出∠2=∠3,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠A+∠ADC=180°,∠C+∠ABC=180°,即可得出答案.
解答 解:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC (角平分线定义),
∵∠ABC=∠ADC(已知),
∴$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ADC(等式的性质),
∴∠1=∠3 (等量代换),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠A+∠ADC=180°,∠C+∠ABC=180°(两直线平行,同旁内角互补),
∴∠A=∠C(等角的补角相等),
故答案为:$\frac{1}{2}$∠ADC,角平分线定义,等式的性质.
点评 本题考查了平行线的性质和判定,角平分线定义等知识点,能灵活运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.

练习册系列答案
相关题目
15. 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | 1<|a|<b | B. | 1<-a<b | C. | |a|<1<|b| | D. | -b<a<-1 |
 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1)



 按下列要求画图并填空:
按下列要求画图并填空: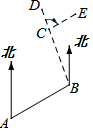 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.
如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.