题目内容
2.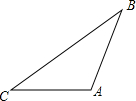 实践与操作:如图,在△ABC中,AB=3,∠C=30°.
实践与操作:如图,在△ABC中,AB=3,∠C=30°.(1)尺规作图:作△ABC的外接圆⊙O;(要求:保留作图痕迹,不写作法)
(2)在你按(1)中要求所作的图中,画⊙O的切线BF,BF与CA的延长线交于点F,若CF⊥BF,求BC的长.
分析 (1)分别作AC和BC的垂直平分线,它们相交于点O,则以O为圆心,OA为半径作圆即可;
(2)连接OA、OB,OA交BC于E,如图,根据切线的性质得OB⊥BF,再证明OB∥CF得到∠OBC=∠C=30°,利用圆周角定理得到∠AOB=2∠C=60°,于是可判定△OAB为等边三角形,所以∠ABC=30°,则可判断BC平分∠ABO,根据等边三角形的性质得AO⊥BC,利用垂径定理得到BE=CE,然后在Rt△ACE中,利用含30度的直角三角形三边的关系求出BE,从而得到BC的长.
解答 解:(1)如图,⊙O为所作;
(2)连接OA、OB,OA交BC于E,如图,
∵BF为切线,
∴OB⊥BF,
∵BF⊥CF,
∴OB∥CF,
∴∠OBC=∠C=30°,
∵∠AOB=2∠C=60°,
∵OA=OB,
∴△OAB为等边三角形,
∴∠ABC=30°,
∴BC平分∠ABO,
∴AO⊥BC,
∴BE=CE,
在Rt△ACE中,AE=$\frac{1}{2}$AB=$\frac{3}{2}$,
BE=$\sqrt{3}$AE=$\frac{3\sqrt{3}}{2}$,
∴BC=2BE=3$\sqrt{3}$.
点评 本题考查了作与-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解决(2)小题的关键是判断△OAB为等边三角形.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
12.下列运算正确的是( )
| A. | a2+a2=a4 | B. | a6÷a3=a2 | C. | (a3b)2=a5b3 | D. | a3×a2=a5 |
13.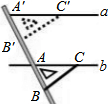 如图,七年级下册数学教材给出了利用直尺和三角板画平行线的方法,能判定画出的直线与已知直线平行的是( )
如图,七年级下册数学教材给出了利用直尺和三角板画平行线的方法,能判定画出的直线与已知直线平行的是( )
 如图,七年级下册数学教材给出了利用直尺和三角板画平行线的方法,能判定画出的直线与已知直线平行的是( )
如图,七年级下册数学教材给出了利用直尺和三角板画平行线的方法,能判定画出的直线与已知直线平行的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BCA=∠B′C′A′ | C. | ∠CAB=∠C′A′B′ | D. | ∠CAA′=∠C′A′A |
10.下列各数中最小的数是( )
| A. | -2 | B. | -π | C. | -$\sqrt{3}$ | D. | 1 |
11.下列计算正确的是( )
| A. | (a2)3=a6 | B. | a2•a3=a6 | C. | (ab)2=ab2 | D. | a6÷a2=a3 |
12.不等式组$\left\{\begin{array}{l}x>0\\ x<1\end{array}\right.$的解集是( )
| A. | 0<x<1 | B. | x>0 | C. | x<1 | D. | 无解 |

