题目内容

5．若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定满足（　　）
A．对角线相等B．对角线互相平分
C．对角线互相垂直D．对角线相等且相互平分

分析 此题要根据矩形的性质和三角形中位线定理求解；首先根据三角形中位线定理知：所得四边形的对边都平行且相等，那么其必为平行四边形，若所得四边形是矩形，那么邻边互相垂直，故原四边形的对角线必互相垂直，由此得解．

解答 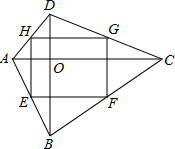解：已知：如右图，四边形EFGH是矩形，且E、F、G、H分别是AB、BC、CD、AD的中点，求证：四边形ABCD是对角线垂直的四边形．
证明：由于E、F、G、H分别是AB、BC、CD、AD的中点，
根据三角形中位线定理得：EH∥FG∥BD，EF∥AC∥HG；
∵四边形EFGH是矩形，即EF⊥FG，
∴AC⊥BD，
故答案为：对角线互相垂直．

点评 本题主要考查了矩形的性质和三角形中位线定理，解题的关键是构造三角形利用三角形的中位线定理解答．

练习册系列答案
相关题目
15．下列运算正确的是（　　）
A．x3+x3=x6B．x6÷x2=x3C．xm•xn=xmnD．（-x5）4=x20
16．已知：在△ABC中，AB=AC，求作：△ABC的内心O．以下是甲、乙两同学的作法：
对于两人的作法，正确的是（　　）
A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对
13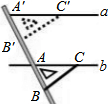．如图，七年级下册数学教材给出了利用直尺和三角板画平行线的方法，能判定画出的直线与已知直线平行的是（　　）
A．∠ABC=∠A′B′C′B．∠BCA=∠B′C′A′C．∠CAB=∠C′A′B′D．∠CAA′=∠C′A′A
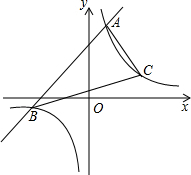20．已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A，B两点，当x＞1，时，y1＞y2；当0＜x＜1时，y1＜y2．
（1）求一次函数的解析式；
（2）如果双曲线上有一点C，使△ABC是直角三角形，那么符合条件的点C有4个，如果点C在双曲线的第一象限上，且∠ACB=90°，求Rt△ABC外接圆的半径．
10．下列各数中最小的数是（　　）
A．-2B．-πC．-$\sqrt{3}$D．1
17．为判断命题“有三条边相等且一组对角相等的四边形是菱形”的真假，数学课上，老师给出菱形ABCD，并作出了一个四边形ABC′D，具体作图过程如下：如图，在菱形ABCD中，
①连接BD，以点B为圆心，以BD的长为半径作圆弧，交CD于点P；
②分别以B、D为圆心，以BC、PC的长为半径作圆弧，两弧交于点C′；
③连接BC′、DC′，得四边形ABC′D．
依据上述作图过程，解决以下问题：
求证：∠A=∠C′；AD=BC′．
14．已知关于x的一元二次方程x2-3x+m-3=0．
（1）若此方程有两个不相等的实数根，求m的取值范围；
（2）若此方程的两根互为倒数，求m的值．
15．如图，抛物线y=-x2+bx+c与x轴交于点A（-1，0）、B（3，0）．
（1）求b、c的值；
（2）如图1直线y=kx+1（k＞0）与抛物线第一象限的部分交于D点，交y轴于F点，交线段BC于E点．求$\frac{DE}{EF}$的最大值；
（3）如图2，抛物线的对称轴与抛物线交于点P、与直线BC相交于点M，连接PB．问在直线BC下方的抛物线上是否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网