题目内容
2.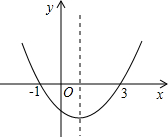 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )| A. | 对称轴是直线x=1 | B. | 方程ax2+bx+c=0的解是x1=-1,x2=3 | ||
| C. | 当x<1,y随x的增大而增大 | D. | 当-1<x<3时,y<0 |
分析 由图象与x轴的交点坐标即可判定下列说法是否正确.
解答 解:∵抛物线与x轴交点的横坐标分别为-1、3,
∴对称轴是直线x=$\frac{-1+3}{2}$=1,方程ax2+bx+c=0的解是x1=-1,x2=3,故A、B正确;
∵抛物线y=ax2+bx+c(a≠0)的开口向上,
∴当x<1,y随x的增大而减小,故C错误;
∵当-1<x<3时,抛物线在x轴的下面,
∴y<0,故D正确,
故选C.
点评 此题考查了抛物线和x轴的交点坐标问题,解题的关键是正确的识别图象.

练习册系列答案
相关题目
7.甲,乙两班进行跳绳比赛,参赛学生每分跳绳的个数统计结果如下表:
某同学分析上表后得出如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳的个数≥150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
| 班级 | 参赛人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳的个数≥150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
14.下列调查,不适合做全面调查的是( )
| A. | 审查一篇书稿有哪些科学性错误 | |
| B. | 了解你所在班级全体同学的视力情况 | |
| C. | 对乘坐飞机的旅客是否带违禁品的调查 | |
| D. | 了解某工厂生产出的一批轮胎的最大承受力 |
11.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
| 统计量 | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差 | 0.60 | 0.62 | 0.50 | 0.44 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
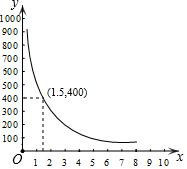 码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图.
码头工人往一艘轮船上装载货物,装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图. 如图,AB=AC,且AB⊥AC,若C(0,-1),B(-4,0),求点A坐标.
如图,AB=AC,且AB⊥AC,若C(0,-1),B(-4,0),求点A坐标. 已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.