题目内容
7. 已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
分析 根据数轴和题目中的式子可以求得c-b的值,从而可以求得|b-c|的值.
解答 解:∵|a-c|=10,|a-d|=12,|b-d|=9,
∴c-a=10,d-a=12,d-b=9,
∴(c-a)-(d-a)+(d-b)
=c-a-d+a+d-b
=c-b
=10-12+9=7,
∵|b-c|=c-b,
∴|b-c|=7,
故答案为:7.
点评 本题考查数轴、绝对值,解答本题的关键是明确数轴的特点,可以将绝对值符号去掉,求出相应的式子的值.

练习册系列答案
相关题目
2.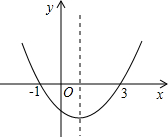 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
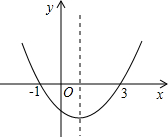 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )| A. | 对称轴是直线x=1 | B. | 方程ax2+bx+c=0的解是x1=-1,x2=3 | ||
| C. | 当x<1,y随x的增大而增大 | D. | 当-1<x<3时,y<0 |
20.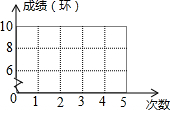 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
某同学计算出了甲的成绩平均数是9,方差是
S甲2=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=17;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.
 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
S甲2=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=17;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.
17.下列运算正确的是( )
| A. | (-a)4=a4 | B. | 8a-a=8 | C. | a3×a2=a6 | D. | (a-b)2=a2-b2 |
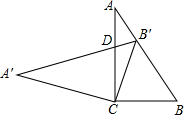 在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.
在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.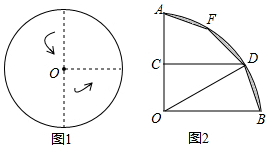 如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.