题目内容
11．甲、乙、丙、丁四人进行射击测试，记录每人10次射击成绩，得到各人的射击成绩平均数和方差如表中所示，则成绩最稳定的是（ ）| 统计量 | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差 | 0.60 | 0.62 | 0.50 | 0.44 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
分析 根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
解答 解：∵每人10次射击成绩的平均数均是9.2环，方差依次为0.60、0.62、0.50、0.44，
∴丁的方差最小，
∴成绩最稳定的是丁；
故选D．
点评 本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
练习册系列答案
名校课堂系列答案
相关题目
1．下列运算正确的是（ ）
| A． | （a2+2b2）-2（-a2+b2）=3a2+b2 | B． | $\frac{{a}^{2}+1}{a-1}$-a-1=$\frac{2a}{a-1}$ | ||
| C． | （-a）3m÷am=（-1）ma2m | D． | 6x2-5x-1=（2x-1）（3x-1） |
2．
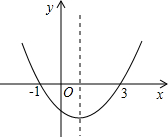如图，抛物线y=ax2+bx+c（a≠0）的开口向上，与x轴交点的横坐标分别为-1、3，则下列说法错误的是（ ）
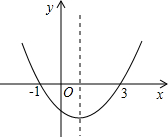如图，抛物线y=ax2+bx+c（a≠0）的开口向上，与x轴交点的横坐标分别为-1、3，则下列说法错误的是（ ）| A． | 对称轴是直线x=1 | B． | 方程ax2+bx+c=0的解是x1=-1，x2=3 | ||
| C． | 当x＜1，y随x的增大而增大 | D． | 当-1＜x＜3时，y＜0 |
19．下列计算正确的是（ ）
| A． | $\sqrt{（-4）^{2}}$=2 | B． | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | C． | （$\sqrt{2}$）2=4 | D． | $\sqrt{6}$÷$\sqrt{2}$=3 |
6．下列运算可直接运用平方差公式的是（ ）
| A． | （a+b）（-a+b） | B． | （a+b）（-a-b） | C． | （a+b）（b+a） | D． | （a-b）（b-a） |
16．已知点A（1，y1），B（2，y2），C（-3，y3）都在反比例函数y=$\frac{{{k^2}+1}}{x}$的图象上，则y1，y2，y3的大小关系是（ ）
| A． | y3＜y1＜y2 | B． | y1＜y2＜y3 | C． | y2＜y1＜y3 | D． | y3＜y2＜y1 |
20．
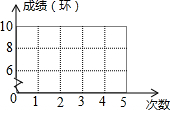甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：
某同学计算出了甲的成绩平均数是9，方差是
S甲2=$\frac{1}{5}$[（10-9）2+（8-9）2+（9-9）2+（10-9）2+（8-9）2]=0.8，请作答：
（1）在图中用折线统计图将甲运动员的成绩表示出来；
（2）若甲、乙射击成绩平均数都一样，则a+b=17；
（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．
甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：| 运动员 环数 次数 | 1 | 2 | 3 | 4 | 5 |
| 甲 | 10 | 8 | 9 | 10 | 8 |
| 乙 | 10 | 9 | 9 | a | b |
S甲2=$\frac{1}{5}$[（10-9）2+（8-9）2+（9-9）2+（10-9）2+（8-9）2]=0.8，请作答：
（1）在图中用折线统计图将甲运动员的成绩表示出来；
（2）若甲、乙射击成绩平均数都一样，则a+b=17；
（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a、b的所有可能取值，并说明理由．
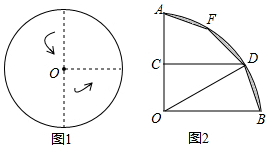如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交$\widehat{AB}$于点D，点F是$\widehat{AB}$上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为36π-108．