��Ŀ����
7���ף������������������������ѧ��ÿ�������ĸ���ͳ�ƽ�����±���| �༶ | �������� | ��λ�� | ���� | ƽ������ |
| �� | 55 | 149 | 191 | 135 |
| �� | 55 | 151 | 110 | 135 |
�ټס�������ѧ����ƽ���ɼ���ͬ��
���Ұ�������������ڼװ������������ÿ���������ĸ�����150Ϊ���㣩��
�ۼװ�ɼ��IJ������Ұ��������������ȷ���ǣ�������
| A�� | �٢ڢ� | B�� | �٢� | C�� | �٢� | D�� | �ڢ� |
���� ƽ��ˮƽ���ж���Ҫ����ƽ�����������������жϴ���λ����ͬ���Եõ���������С�ȽϷ���Ĵ�С��
��� �⣺�ӱ��п�֪��ƽ����������135������ȷ��
�װ����λ����149���Ұ����λ����151���ȼĶ࣬��ƽ������ҪΪ135��˵���ҵ������������ڼװ�ģ�����ȷ��
�װ�ķ�������Ұ�ģ���˵���װ�IJ�����������Ԣ�Ҳ��ȷ��
��ѡA��
���� ���⿼����ƽ��������λ������������壮ƽ����ƽ������ʾһ�����ݵ�ƽ���̶ȣ���λ���ǽ�һ�����ݴ�С����Ӵ�С���������к����м���Ǹ����������м���������ƽ����������������������һ�����ݲ�����С������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
18������$\frac{{{{��{x+y}��}^2}-{{��{x-y}��}^2}}}{4xy}$�Ľ��Ϊ��������
| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{4}$ | D�� | 0 |
2��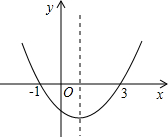 ��ͼ��������y=ax2+bx+c��a��0���Ŀ������ϣ���x�ύ��ĺ�����ֱ�Ϊ-1��3��������˵��������ǣ�������
��ͼ��������y=ax2+bx+c��a��0���Ŀ������ϣ���x�ύ��ĺ�����ֱ�Ϊ-1��3��������˵��������ǣ�������
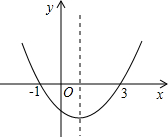 ��ͼ��������y=ax2+bx+c��a��0���Ŀ������ϣ���x�ύ��ĺ�����ֱ�Ϊ-1��3��������˵��������ǣ�������
��ͼ��������y=ax2+bx+c��a��0���Ŀ������ϣ���x�ύ��ĺ�����ֱ�Ϊ-1��3��������˵��������ǣ�������| A�� | �Գ�����ֱ��x=1 | B�� | ����ax2+bx+c=0�Ľ���x1=-1��x2=3 | ||
| C�� | ��x��1��y��x����������� | D�� | ��-1��x��3ʱ��y��0 |
12��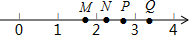 ��ͼ��M��N��P��Q�������ϵ��ĸ��㣬���ĸ��������ʺϱ�ʾ$\sqrt{7}$���ǣ�������
��ͼ��M��N��P��Q�������ϵ��ĸ��㣬���ĸ��������ʺϱ�ʾ$\sqrt{7}$���ǣ�������
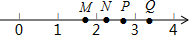 ��ͼ��M��N��P��Q�������ϵ��ĸ��㣬���ĸ��������ʺϱ�ʾ$\sqrt{7}$���ǣ�������
��ͼ��M��N��P��Q�������ϵ��ĸ��㣬���ĸ��������ʺϱ�ʾ$\sqrt{7}$���ǣ�������| A�� | M�� | B�� | N�� | C�� | P�� | D�� | Q�� |
19�����м�����ȷ���ǣ�������
| A�� | $\sqrt{��-4��^{2}}$=2 | B�� | $\sqrt{2}$��$\sqrt{5}$=$\sqrt{10}$ | C�� | ��$\sqrt{2}$��2=4 | D�� | $\sqrt{6}$��$\sqrt{2}$=3 |
16����֪��A��1��y1����B��2��y2����C��-3��y3�����ڷ���������y=$\frac{{{k^2}+1}}{x}$��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵ�ǣ�������
| A�� | y3��y1��y2 | B�� | y1��y2��y3 | C�� | y2��y1��y3 | D�� | y3��y2��y1 |
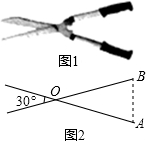 ��ͼ1��һ���ּ�������������Ϊͼ2������OA=OB���������ſ��Ľ�Ϊ30�㣬���A=75�ȣ�
��ͼ1��һ���ּ�������������Ϊͼ2������OA=OB���������ſ��Ľ�Ϊ30�㣬���A=75�ȣ�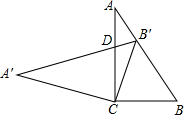 ��Rt��ABC�У���C=90�㣬cosB=0.6�������ֱ���������ƶ���C��ת��õ�Rt��A'B'C�����е�B'��������AB�ϣ�A'B'��AC�ཻ�ڵ�D����ôB��D��CD=0.35��
��Rt��ABC�У���C=90�㣬cosB=0.6�������ֱ���������ƶ���C��ת��õ�Rt��A'B'C�����е�B'��������AB�ϣ�A'B'��AC�ཻ�ڵ�D����ôB��D��CD=0.35��