题目内容
 矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求△DEF的面积.
矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求△DEF的面积.考点:矩形的性质,全等三角形的判定与性质,等腰直角三角形
专题:
分析:先设AD=x.由△DEF为等腰直角三角形,可以得到一对边相等,一对角相等,再加上一对直角相等,那么△ADE和△BEF全等,就有AD=BE.那么利用边相等可得x+x+2=10,解之即得AD,根据勾股定理求得DE2,即可求得△DEF的面积.
解答:解:先设AD=x.
∵△DEF为等腰三角形.
∴DE=EF,∠FEB+∠DEA=90°.
又∵∠AED+∠ADE=90°.
∴∠FEB=∠EDA.
又∵四边形ABCD是矩形,
∴∠B=∠A=90°.
在△ADE和△BEF中
,
∴△ADE≌△BEF(AAS).
∴AD=BE.
∴AD+CD=AD+AB=x+x+2=10.
解得x=4.
即AD=4.
在RT△ADE中,DE2=AD2+AE2=42+22=20,
∵S=
DE•EF=
DE2=
×20=10.
∴△DEF的面积为10.
∵△DEF为等腰三角形.
∴DE=EF,∠FEB+∠DEA=90°.
又∵∠AED+∠ADE=90°.
∴∠FEB=∠EDA.
又∵四边形ABCD是矩形,
∴∠B=∠A=90°.
在△ADE和△BEF中
|
∴△ADE≌△BEF(AAS).
∴AD=BE.
∴AD+CD=AD+AB=x+x+2=10.
解得x=4.
即AD=4.
在RT△ADE中,DE2=AD2+AE2=42+22=20,
∵S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△DEF的面积为10.
点评:本题综合考查了等腰直角三角形的性质,同角的余角相等,全等三角形的判定和性质及矩形的性质等知识.

练习册系列答案
相关题目
若a增加x%后得到b,那么b等于( )
| A、ax% |
| B、a(1-x%) |
| C、a+x% |
| D、a(1+x%) |
如图,水平地面上有一面积为30cm2的扇形AOB,半径OA=6cm,且OA与地面垂直,在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动的距离为( )
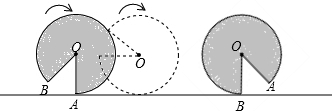

| A、20cm | B、24cm |
| C、10cm | D、30cm |
 如图,四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,过A、B、C三点的⊙O与CD相切于点C,交AD于点G,点E为
如图,四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,过A、B、C三点的⊙O与CD相切于点C,交AD于点G,点E为
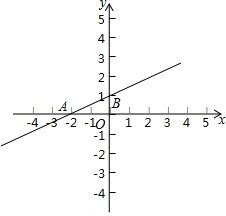 如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).
如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).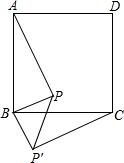 如图所示,在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B,已知正方形ABCD的面积为64cm2,AP=6cm,则PP′=
如图所示,在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B,已知正方形ABCD的面积为64cm2,AP=6cm,则PP′= 如图,四边形ABCD是矩形,∠1=∠2,∠DEC=90°.
如图,四边形ABCD是矩形,∠1=∠2,∠DEC=90°. 把一块含60°的三角板与一把直尺按如图方式放置,则∠α=
把一块含60°的三角板与一把直尺按如图方式放置,则∠α=