Question

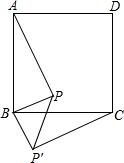如图所示，在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B，已知正方形ABCD的面积为64cm²，AP=6cm，则PP′=

 

．

Answer 1

考点：旋转的性质,勾股定理,等腰直角三角形

专题：

分析：首先求出正方形的边长，再利用勾股定理得出BP的长，即可得出PP′的长．

解答：解：∵在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B，正方形ABCD的面积为64cm²，
∴AB=BC=8cm，BP=BP′，
∵AP=6cm，
∴在Rt△ABP中，BP=

82-62

=2

7

（cm），
则PP′=

BP2+BP′2

=2

14

（cm）．
故答案为：2

14

cm．

点评：此题主要考查了旋转的性质以及勾股定理等知识，得出BP的长是解题关键．