Question

9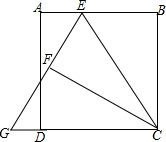．如图，矩形ABCD中，BC=3，且BC＞AB，E为AB边上任意一点（不与A，B重合），设BE=t，将△BCE沿CE对折，得到△FCE，延长EF交CD的延长线于点G，则tan∠CGE=$\frac{6t}{9-{t}^{2}}$（用含t的代数式表示）．

Answer 1

分析 连接BF交EC于O，作EM⊥CD于M，因为tan∠CGE=$\frac{EM}{GM}$，所以只要用t的代数式表示EM、GM，由四边形EMCB是矩形可以求出EM，利用△CBF∽△GCE，可以求出GC，这样即可解决问题．

解答 解：如图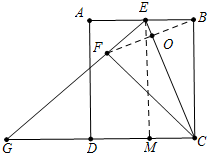连接BF交EC于O，作EM⊥CD于M，
∵∠EMC=∠EBC=∠BCM=90°，
∴四边形EBCM是矩形，
∴CM=EB=t，EM=BC=3，
在RT△EBC中，∵EB=t，BC=3，
∴EC=$\sqrt{{t}^{2}+{3}^{2}}$=$\sqrt{{t}^{2}+9}$，
∵EB=EF，CB=CF，
∴EC垂直平分BF，
∵$\frac{1}{2}$•EC•BO=$\frac{1}{2}$•EB•BC，
∴BO=$\frac{3t}{\sqrt{{t}^{2}+9}}$，BF=2BO=$\frac{6t}{\sqrt{{t}^{2}+9}}$
∵∠AEF+∠BEF=180°，∠BEF+∠BCF=180°，
∴∠AEF=∠BCF，
∵AB∥CD，
∴∠BEC=∠ECG=∠CEF，∠AEF=∠G=∠BCF
∴GE=GC，
∴∠GCE=∠GEC=∠CFB=∠CBF，
∴△CBF∽△GCE，
∴$\frac{GC}{BC}=\frac{EC}{BF}$，
∴GC=$\frac{{t}^{2}+9}{2t}$，GM=GC-CM=$\frac{9-{t}^{2}}{2t}$，
∴tan∠CGE=$\frac{EM}{GM}$=$\frac{6t}{9-{t}^{2}}$．
故答案为$\frac{6t}{9-{t}^{2}}$．

点评 本题考查翻折变换、矩形的性质、相似三角形的判定和性质，学会利用翻折不变性找到相等的边以及角，添加辅助线构造相似三角形是解决问题的关键，属于中考常考题型．