题目内容
19.已知四边形ABCD中,∠BAD=90°,AB=8cm,以A,B,C三点为顶点的三角形是一个等边三角形,以A,C,D三点为顶点的三角形是一个直角三角形,求四边形ABCD的面积.分析 首先对图形进行分析,当∠ADC=90°和当ACD=90°,所画图形不同,再利用勾股定理可以求出三角形ABC的面积,再利用解直角三角形的知识求出AD,CD,从而得出三角形面积,从而得出答案.
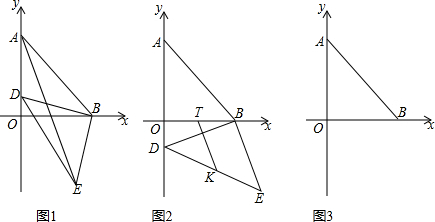
解答  解:①如图1,作AE⊥BC于点E,
解:①如图1,作AE⊥BC于点E,
当∠ADC=90°,
∵△ABC为等边三角形,
∴AB=AC=BC=8,
∴EC=4,
∴AE=4$\sqrt{3}$,
∠BAC=60°,
∵∠BAD=90,
∴∠CAD=90°-60°=30°,
在Rt△ACD中,
CD=$\frac{1}{2}$AC=4,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=4$\sqrt{3}$,
S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×BC×AE+$\frac{1}{2}$CD×AD,
=$\frac{1}{2}$×4$\sqrt{3}$×8+$\frac{1}{2}$×4$\sqrt{3}$×4,
=20$\sqrt{3}$;
②如图2,当∠ACD=90°,
∵AC=8,∠BAD=90°,
∴∠CAD=30°,
∴tan30°=$\frac{CD}{AC}$,
解得:CD=$\frac{8\sqrt{3}}{3}$,
S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×BC×AE+$\frac{1}{2}$CD×AC,
=$\frac{1}{2}$×4$\sqrt{3}$×8+$\frac{1}{2}$×$\frac{8\sqrt{3}}{3}$×8,
=$\frac{80\sqrt{3}}{3}$.
点评 此题主要考查了勾股定理与解直角三角形的应用,根据已知进行分类讨论得出两种情况,这种思想经常运用与数学运算与证明,同学们应熟练掌握此知识.

练习册系列答案
相关题目
14.$\sqrt{6}$-3的绝对值是( )
| A. | $\sqrt{6}$-3 | B. | -$\sqrt{6}$-3 | C. | 3-$\sqrt{6}$ | D. | $\frac{1}{\sqrt{6}-3}$ |
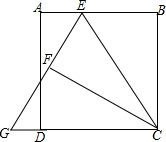 如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).