题目内容
4.设P=a2b2+5,Q=2ab-a2-4a,若P=Q,则a+b=-$\frac{5}{2}$.分析 根据P=Q可得a2b2+5=2ab-a2-4a,将右边整式全部移到左边后把5拆成1+4,根据完全平方公式配方,由非负数性质可得a、b的值即可.
解答 解:根据题意,可得:a2b2+5=2ab-a2-4a,
即:a2b2-2ab+1+a2+4a+4=0,
∴(ab-1)2+(a+2)2=0,
∵(ab-1)2≥0,且(a+2)2≥0,
∴ab-1=0,a+2=0,
即a=-2,b=-$\frac{1}{2}$,
则a+b=-$\frac{5}{2}$,
故答案为:-$\frac{5}{2}$.
点评 本题主要考查完全平方公式的掌握与运用,根据题意得到关于a、b的方程后移项、配方是本题的关键,由非负数性质求得a、b的值是根本.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
13.把P1(2,$\sqrt{3}$)向下平移$\sqrt{3}$个单位长度再向左平移2个单位长度到达点P2处,则P2的坐标是( )
| A. | (4,0) | B. | (0,0) | C. | (2,2$\sqrt{3}$) | D. | (4,$\sqrt{3}$) |
14.$\sqrt{6}$-3的绝对值是( )
| A. | $\sqrt{6}$-3 | B. | -$\sqrt{6}$-3 | C. | 3-$\sqrt{6}$ | D. | $\frac{1}{\sqrt{6}-3}$ |
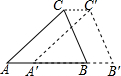 如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.
如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.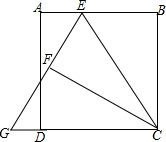 如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示). 端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.
端午节间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的方差=5.35.