题目内容
14.若a+b=3,ab=-7,则$\frac{a}{b}+\frac{b}{a}$的值为( )| A. | -$\frac{14}{5}$ | B. | -$\frac{2}{5}$ | C. | -$\frac{23}{7}$ | D. | -$\frac{25}{7}$ |
分析 先根据分式混合运算的法则把原式进行化简,再把a+b=3,ab=-7代入进行计算即可.
解答 解:原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$,
∵a+b=3,ab=-7,
∴原式=$\frac{{3}^{2}-2×(-7)}{-7}$=$\frac{9+14}{-7}$=-$\frac{23}{7}$.
故选C.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.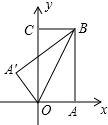 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )| A. | $(-\frac{3}{5},\frac{4}{5})$ | B. | $(-\frac{2}{5},\frac{4}{5})$ | C. | $(-\frac{4}{5},\frac{3}{5})$ | D. | $(-\frac{2}{5},\frac{3}{5})$ |
4.若等式2□(-1)=3成立,则“□”内的运算符号是( )
| A. | + | B. | - | C. | × | D. | ÷ |
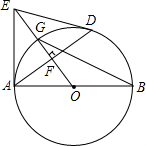 如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长.
如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长.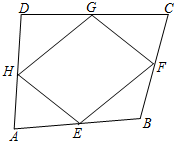 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.