题目内容
2.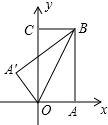 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )| A. | $(-\frac{3}{5},\frac{4}{5})$ | B. | $(-\frac{2}{5},\frac{4}{5})$ | C. | $(-\frac{4}{5},\frac{3}{5})$ | D. | $(-\frac{2}{5},\frac{3}{5})$ |
分析 由已知条件可得:BC=1,OC=2.设OC与A′B交于点F,作A′E⊥OC于点E,易得△BCF≌△OA′F,那么OA′=BC=1,设A′F=x,则OF=2-x.利用勾股定理可得A′F=$\frac{3}{4}$,OF=$\frac{5}{4}$,利用面积可得A′E=A′F×OA′÷OF=$\frac{3}{5}$,利用勾股定理可得OE=$\frac{4}{5}$,所以点A’的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$).
解答 解:∵OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,
∴BC=1,OC=2,
如图,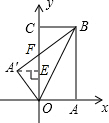
设OC与A′B交于点F,作A′E⊥OC于点E,
∵纸片OABC沿OB折叠
∴OA=OA′,∠BAO=∠BA′O=90°,
∵BC∥A′E,
∴∠CBF=∠FA′E,
∵∠AOE=∠FA′O,
∴∠A′OE=∠CBF,
∴△BCF≌△OA′F,
∴OA′=BC=1,设A′F=x,
∴OF=2-x,
∴x2+1=(2-x)2,
解得x=$\frac{3}{4}$,∴A′F=$\frac{3}{4}$,OF=$\frac{5}{4}$,
∵A′E=A′F×OA′÷OF=$\frac{3}{5}$,
∴OE=$\frac{4}{5}$,
∴点A′的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$)..
故选:A.
点评 此题考查折叠的性质,解决本题的关键是利用三角形的全等得到点A′所在的三角形的一些相关的线段的长度,进而利用面积的不同表示方法和勾股定理得到所求的点的坐标.

练习册系列答案
相关题目
14.若a+b=3,ab=-7,则$\frac{a}{b}+\frac{b}{a}$的值为( )
| A. | -$\frac{14}{5}$ | B. | -$\frac{2}{5}$ | C. | -$\frac{23}{7}$ | D. | -$\frac{25}{7}$ |
11.在下列运算中,正确的是( )
| A. | a2+a3=2a5 | B. | (a2)3=a6 | C. | a6÷a2=a3 | D. | a2•a3=a6 |