题目内容
9.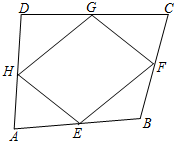 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.
分析 根据三角形中位线定理证明EF=$\frac{1}{2}$AC,EF∥AC,GH=$\frac{1}{2}$AC,GH∥AC,得到四边形EFGH是平行四边形,根据邻边相等的平行四边形是菱形得到答案.
解答 解:四边形ABCD还应满足的一个条件是AC=BD,
证明: ∵E、F分别是AB、BC的中点,
∵E、F分别是AB、BC的中点,
∴EF=$\frac{1}{2}$AC,EF∥AC,
∵G、H分别是CD、DA的中点,
∴GH=$\frac{1}{2}$AC,GH∥AC,
∴四边形EFGH是平行四边形,
∵F、G分别是BC、CD的中点,
∴GF=$\frac{1}{2}$BD,又AC=BD,
∴EF=GF,
∴四边形EFGH是菱形,
故答案为:AC=BD.
点评 本题考查的是中点四边形,掌握平行四边形的判定定理、菱形的判定定理是解题的关键,注意邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
20.如果把分式$\frac{x+y}{2y}$中的x、y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 扩大6倍 | C. | 扩大3倍 | D. | 不变 |
14.若a+b=3,ab=-7,则$\frac{a}{b}+\frac{b}{a}$的值为( )
| A. | -$\frac{14}{5}$ | B. | -$\frac{2}{5}$ | C. | -$\frac{23}{7}$ | D. | -$\frac{25}{7}$ |
1.设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系.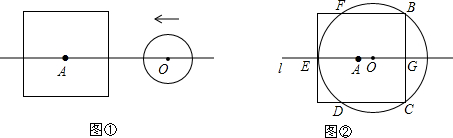
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
(1)如图①,当r<a时,填表:
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
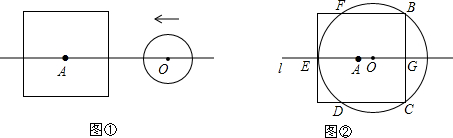
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
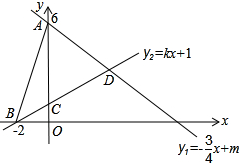 已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求:
已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求: 已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.