题目内容
6.先化简再求值:(1)4(m+1)2-(2m+5)(2m-5),其中m=-3.
(2)$\frac{{x}^{2}-1}{x}$+(1-$\frac{2x-1}{x}$),其中x=$\sqrt{2}$.
分析 (1)先根据整式混合运算的法则把原式进行化简,再把m=-3代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x=$\sqrt{2}$代入进行计算即可.
解答 解:(1)原式=4(m2+2m+1)-(4m2-25)
=4m2+8m+4-4m2-25
=8m-21,
当m=-3时,原式=-24-21=-45;
(2)原式=$\frac{{x}^{2}-1}{x}$+$\frac{x-2x+1}{x}$
=$\frac{{x}^{2}-1}{x}$+$\frac{-x+1}{x}$
=$\frac{{x}^{2}-1-x+1}{x}$
=$\frac{x(x-1)}{x}$
=x-1,
当x=$\sqrt{2}$时,原式=$\sqrt{2}$-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
16.一个数的相反数比本身大,那么这个数必定是( )
| A. | 正数 | B. | 负数 | C. | 整数 | D. | 0 |
14.若a+b=3,ab=-7,则$\frac{a}{b}+\frac{b}{a}$的值为( )
| A. | -$\frac{14}{5}$ | B. | -$\frac{2}{5}$ | C. | -$\frac{23}{7}$ | D. | -$\frac{25}{7}$ |
1.设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系.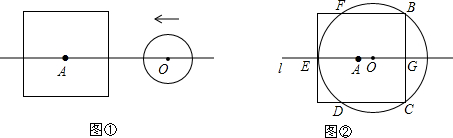
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
(1)如图①,当r<a时,填表:
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
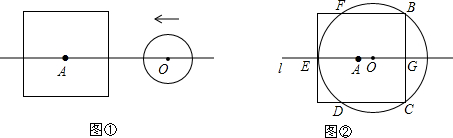
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
11.在下列运算中,正确的是( )
| A. | a2+a3=2a5 | B. | (a2)3=a6 | C. | a6÷a2=a3 | D. | a2•a3=a6 |
15.当关于x的方程2x-1=ax+2的解为x=-1时,那么a的值为( )
| A. | -1 | B. | -2 | C. | -5 | D. | 5 |