题目内容
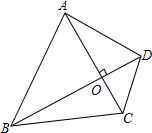 如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.
如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)根据(1)中的函数关系式,求出当x为何值时S最大,并求出最大值.
考点:二次函数的最值
专题:
分析:(1)根据已知得出四边形ABCD面积为S,则BD=10-x,进而求出S=-
x2+5x;
(2)根据二次函数的顶点坐标来求其最值.
| 1 |
| 2 |
(2)根据二次函数的顶点坐标来求其最值.
解答:解:(1)设AC=x,四边形ABCD面积为S,则BD=10-x
S=
x(10-x)=-
x2+5x,
即S=-
x2+5x;
(2)∵a=-
<0,
∴S有最大值
当x=-
=5时,S最大=
=
.
S=
| 1 |
| 2 |
| 1 |
| 2 |
即S=-
| 1 |
| 2 |
(2)∵a=-
| 1 |
| 2 |
∴S有最大值
当x=-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 25 |
| 2 |
点评:此题主要考查了二次函数的应用,根据已知正确得出二次函数关系是解题关键.

练习册系列答案
相关题目
下列各数中,互为倒数的是( )
| A、0和0 | ||
| B、1和-1 | ||
| C、-1和-1 | ||
D、-0.75与-
|
矩形具有而平行四边形不一定具有的特征是( )
| A、对角线互相平分 |
| B、对角线相等 |
| C、两组对角相等 |
| D、两组对边平行且相等 |
 如图,直线为一次函数y=kx+b的图象,则当y<0时,则x
如图,直线为一次函数y=kx+b的图象,则当y<0时,则x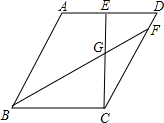 如图,在?ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
如图,在?ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.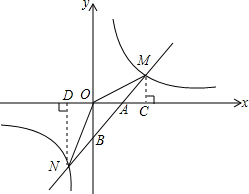 如图,已知反比例函数y=
如图,已知反比例函数y=
