题目内容
14. 如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.
如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.
分析 首先过点M作ME∥AB,交BC于点E,过点M作MF∥CD,交BC于点F,易证得四边形ABEM与四边形DCFM是平行四边形,△EMF是直角三角形,然后由直角三角形斜边上的中线等于斜边的一半,求得MN的长.
解答 解:过点M作ME∥AB,交BC于点E,过点M作MF∥CD,交BC于点F,
∵AD∥BC,
∴四边形ABEM与四边形DCFM是平行四边形,
∴BE=AM,CF=DM,ME=AB,MF=DC,
∴EF=BC-BE-CF=BC-AM-DM=BC-AD=10-4=6,
∵AB=DC,
∴ME=MF,
∵∠C=36°,∠B=54°,
∴∠MEF=∠C=36°,∠MFE=∠B=54°,
∴∠EMF=90°,
∵M、N分别是AD、BC的中点,
∴EN=FN=MN,
∴MN=$\frac{1}{2}$EF=3.
故答案为:3.
点评 此题考查了等腰梯形的性质、平行四边形的判定与性质以及直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
4.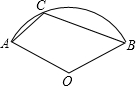 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )| A. | 240° | B. | 120° | C. | 90° | D. | 75° |
2.湖南省2017年公务员录用考试是这样统计成绩的,综合成绩=笔试成绩×60%+面试成绩×40%,小红姐姐的笔试成绩是82分,她的竞争对手的笔试成绩是86分,小红姐姐要使自己的综合成绩追平竞争对手,则她的面试成绩必须比竞争对手多( )
| A. | 2.4分 | B. | 4分 | C. | 5分 | D. | 6分 |
9.已知α为锐角,且tan(90°-α)=$\sqrt{3}$,则α的度数为( )
| A. | 30° | B. | 60° | C. | 45° | D. | 75° |
6.下列函数中,y是x的一次函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=2x+11 | C. | y=x2+x+1 | D. | y=$\frac{1}{x}$ |
 如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分
如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分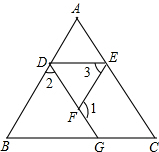 如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由.
如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由. 如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.
如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.