题目内容
5. 如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分
如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,求证:
(1)△ACF≌△ADF;
(2)FG=FE.
分析 (1)根据已知,利用SAS判定△ACF≌△ADF;
(2)已知DF∥BC,AC⊥BC,则GF⊥AC,再根据角平分线上的点到角两边的距离相等得到FG=EF.
解答  (1)证明:∵AF平分∠CAB,
(1)证明:∵AF平分∠CAB,
∴∠CAF=∠DAF.
在△ACF和△ADF中,
∵$\left\{\begin{array}{l}{AC=AD}\\{∠CAF=∠DAF}\\{AF=AF}\end{array}\right.$,
∴△ACF≌△ADF(SAS).
(2)证明:∵DF∥BC,BC⊥AC,
∴FG⊥AC.
∵FE⊥AB,
又AF平分∠CAB,
∴FG=FE.
点评 本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
13. 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
20.若$\sqrt{{a}^{3}+3{a}^{2}}$=-a$\sqrt{a+3}$,则a的取值范围是( )
| A. | -3≤a≤0 | B. | a≤0 | C. | a<0 | D. | a≥-3 |
10.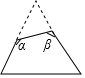 如图,一个顶角为40°的等腰三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
如图,一个顶角为40°的等腰三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
 如图,一个顶角为40°的等腰三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
如图,一个顶角为40°的等腰三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )| A. | 180° | B. | 220° | C. | 240° | D. | 300° |
17.若m>-1,则下列错误的是( )
| A. | 6m>-6 | B. | -5m>5 | C. | m+1>0 | D. | 1-m<2 |
 如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3.
如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3. 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°. 如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.
如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.