题目内容
4.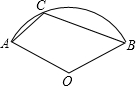 如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )
如图,扇形OAB的圆心角为120°,C是弧AB上一点,则∠ACB的度数为( )| A. | 240° | B. | 120° | C. | 90° | D. | 75° |
分析 在⊙O上取点D,连接AD,BD,根据圆周角定理求出∠D的度数,由圆内接四边形的性质即可得出结论.
解答 解:如图 所示,在⊙O上取点D,连接AD,BD,
所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=120°,
∴∠ADB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120°=60°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°-60°=120°.
故选:B.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.点P(2m-4,3 )在第二象限,则m的取值范围是( )
| A. | m>2 | B. | m<2 | C. | m≥-2 | D. | m≤2 |
13. 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
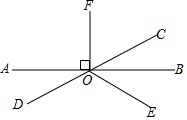 如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O,
如图,已知AB、CD相交于点O,OB平分∠COE,OF⊥AB于O, 如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3.
如图,在矩形ABCD中,E在AD上,F在AB上,且EF⊥EC,EF=EC,DE=2,矩形ABCD的周长为16,则AE的长是3. 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°. 如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.
如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.