题目内容

7．某商场购进一批单价为40元的商品，若按每件50元销售，平均每天可销售90件，市场调查发现，这种商品的销售单价每提高1元，平均每天少销售3件，将销售单价定为多少，才能使每天所获销售利润W最大？最大利润W是多少？

分析 设销售价为x元/件，则每天的销售量为：90-3（x-50）件，根据总利润=单件利润×销售量列出函数关系式，配方成顶点式可得最大值．

解答 解：设销售价为x元/件，则每天的销售量为：90-3（x-50）=-3x+240件，
根据题意，得W=（x-40）（-3x+240）
=-3x2+360x-9600
=-3（x-60）2+1200，
则当x=60时，W取得最大值，最大值为1200元，
答：将销售单价定为60元/件时，才能使每天所获销售利润W最大，最大利润W是1200元．

点评 本题主要考查二次函数的实际应用能力，根据题意表示出其销售量是解此类题目的关键，根据相等关系列出函数关系式并求最大值是考查的主要内容．

练习册系列答案
相关题目
17．如图所示：
（1）直接写出点A的坐标为（-1，2），点A关于x轴的对称点B的坐标为（-1，-2），点B关于y轴的对称点C的坐标为（1，-2）．
（2）画出将线段BC向右平移2个单位，再向上平移4个单位后的线段B′C′，并直接写出B′的坐标．
18．方程组$\left\{\begin{array}{l}{2a-3b=15}\\{3a+5b=32.9}\end{array}\right.$的解为$\left\{\begin{array}{l}{a=9.3}\\{b=3.2}\end{array}\right.$，则方程组$\left\{\begin{array}{l}{2（x+2）-3（y-1）=13}\\{3（x+2）+5（y-1）=30.9}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=7.3}\\{y=4.2}\end{array}\right.$．
15．（$\frac{1}{2}$y-1）2=$\frac{1}{4}$y2-y+1．
2．分解因式：
（1）4x（x-y）2-12（y-x）3；
（2）（a+b）2+6（a+b）+9；
（3）（x2-2xy）2-2y2（2xy-x2）+y4．
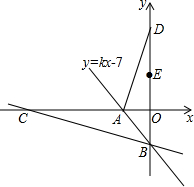12．将直角坐标系中一次函数的图象与坐标轴围成三角形，叫做此一次函数的坐标三角形（也称为直线的坐标三角形）．如图，一次函数y=kx-7的图象与x，y轴分别交于点A，B，那么△ABO为此一次函数的坐标三角形（也称直线AB的坐标三角形）．
（1）如果点C在x轴上，将△ABC沿着直线AB翻折，使点C落在点D（0，18）上，求直线BC的坐标三角形的面积；
（2）如果一次函数y=kx-7的坐标三角形的周长是21，求k的值；
（3）在（1）条件下，如果点E的坐标是（0，8），直线AB上有一点P，使得△PDE周长最小，且点P正好落在某一个反比例函数的图象上，求这个反比例函数的解析式．
19．小华想买一些儿童卡通游戏卡，由于卡片减价20%，用同样多的钱他可以多买5张，小华原来想买多少张儿童卡通游戏卡？
16．已知a+b=50，则a3+150ab+b3的值是（　　）
A．125000B．125001C．125005D．125050
17．关于x的方程x2-mx+2=0的两根和是3，两根积是2，则m的值是（　　）
A．-3B．3C．2D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网