题目内容
14.已知a、b、c为实数,且$\sqrt{a-1}+|b+1|+{(c+3)^2}=0$,求方程ax2+bx+c=0的根.分析 根据已知等式,利用非负数的性质求出a,b,c的值,代入方程计算即可求出解.
解答 解:∵$\sqrt{a-1}$+|b+1|+(c+3)2=0,
∴a=1,b=-1,c=-3,
原方程为x2-x-3=0,
这里a=1,b=-1,c=-3,
∴x=$\frac{1±\sqrt{13}}{2}$.
点评 此题考查了解一元二次方程-公式法,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.下列各式正确的是( )
| A. | 2a+3b=5ab | B. | a+2a=3a2 | C. | 2a2-a2=2 | D. | b2-2b2=-b2 |
2.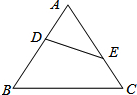 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )| A. | 3 | B. | 12 | C. | $\frac{25}{3}$ | D. | 7 |
9.下列交通标志既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.已知-1是关于x的方程x2+4x-m=0的一个根,则这个方程的另一个根是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
4.若-2amb5与5a2bn-1可以合并成一项,则nm的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 64 |
 如图,△ABC中,∠BAC=60°,D,E两点在直线BC上,连接AD,AE,则∠1+∠2+∠3+∠4=120°.
如图,△ABC中,∠BAC=60°,D,E两点在直线BC上,连接AD,AE,则∠1+∠2+∠3+∠4=120°. 如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒.
如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒.