题目内容
2.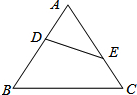 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )| A. | 3 | B. | 12 | C. | $\frac{25}{3}$ | D. | 7 |
分析 由公共角和已知条件证明△ADE∽△ACB,得出对应边成比例,即可求出BC的长.
解答 解:∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}=\frac{AE}{AB}$,
即$\frac{6}{BC}=\frac{5}{10}$,
解得:BC=12.
故选:B.
点评 本题考查了相似三角形的判定与性质;熟练掌握三角形相似的判定与性质,由三角形相似得出比例式是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.点(-2,y1),(-1,y2),(3,y3)均在函数y=-$\frac{6}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y3<y1<y2 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
7.在同一直角坐标系中,一次函数y=2x+1与反比例函数y=$\frac{k}{x}$的图象没有交点,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | k$>-\frac{1}{8}$ | D. | k$<-\frac{1}{8}$ |
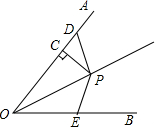 如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.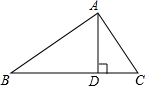 如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.
如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.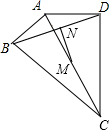 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.
如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.