题目内容
19. 如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒.
如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒.(1)当t=2时,①AB=4cm.②求线段CD的长度.
(2)在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
分析 (1)①根据AB=2t即可得出结论;②先求出BD的长,再根据C是线段BD的中点即可得出CD的长;
(2)直接根据中点公式即可得出结论.
解答 解:(1)①∵B是线段AD上一动点,沿A→D以2cm/s的速度运动,
∴当t=2时,AB=2×2=4cm.
故答案为:4;
②∵AD=10cm,AB=4cm,
∴BD=10-4=6cm,
∵C是线段BD的中点,
∴CD=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3cm;
(2)不变;
∵AB中点为E,C是线段BD的中点,
∴EB=$\frac{1}{2}$AB,BC=$\frac{1}{2}$BD,
∴EC=EB+BC=$\frac{1}{2}$(AB+BD)
=$\frac{1}{2}$AD=$\frac{1}{2}$×10=5cm.
点评 本题考查了两点间的距离,根据已知得出各线段之间的等量关系是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.点(-2,y1),(-1,y2),(3,y3)均在函数y=-$\frac{6}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y3<y1<y2 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
7.在同一直角坐标系中,一次函数y=2x+1与反比例函数y=$\frac{k}{x}$的图象没有交点,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | k$>-\frac{1}{8}$ | D. | k$<-\frac{1}{8}$ |
4.下列方程一定是一元二次方程的是( )
| A. | 2x2-1=3x | B. | 2x2-y=1 | C. | ax2+bx+c=0 | D. | 2x2+$\frac{1}{x}$=1 |
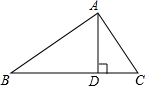 如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.
如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.