题目内容
1.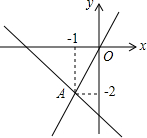 如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.
如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.
分析 由图象可以知道,当x=-1时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式k1x+b<k2x解集.
解答 解:两个条直线的交点坐标为(-1,-2),且当x<-1时,直线y=k2x在y=k1x+b直线的下方,故不等式k1x+b<k2x的解集为x>-1.
故答案为:x>-1.
点评 此题主要考查了一次函数与一元一次不等式,本题是借助一次函数的图象解一元一次不等式,两个图象的“交点”是两个函数值大小关系的“分界点”,在“分界点”处函数值的大小发生了改变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.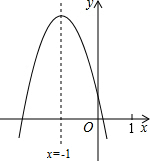 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.实验中学八年级(1)班50名学生参加期末考试,全班学生的数学成绩统计如表:
请根据表中提供的信息解答下列问题:
(1)该班学生这次考试数学成绩的众数是88分;
(2)该班学生这次考试数学成绩的中位数是86分;
(3)该班张华同学在这次考试中的数学成绩是83分,能不能说张华同学的数学成绩处于全班中游偏上水平?试说明理由.
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
(1)该班学生这次考试数学成绩的众数是88分;
(2)该班学生这次考试数学成绩的中位数是86分;
(3)该班张华同学在这次考试中的数学成绩是83分,能不能说张华同学的数学成绩处于全班中游偏上水平?试说明理由.
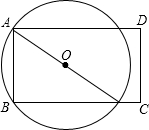 已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.
已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5. 如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$.
如图,如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$.