题目内容
12.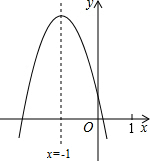 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac<0;②4a+c>2b;③3b+2c<0;④4n(an+b)≤a,其中结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由抛物线与x轴交点个数可判断①;由x=0时y>0及对称轴x=-1可知x=-2时y>0可判断②;由对称轴x=-$\frac{b}{2a}$=-1及x=1时y<0可判断③,假设④成立,通过变形整理可得4n2+8n-1≤0恒成立,由不等式解的情况可判断.
解答 解:由图象可知抛物线与x轴有两个交点,
∴b2-4ac>0,故①错误;
∵抛物线对称轴为x=-1,且当x=0时y>0,
∴当x=-2时,y=4a-2b+c>0,
即4a+c>2b,故②正确;
由抛物线对称轴x=-$\frac{b}{2a}$=-1,可得a=$\frac{b}{2}$,
∵当x=1时,y<0,
∴y=a+b+c<0,
将a=$\frac{b}{2}$代入得:$\frac{b}{2}$+b+c<0,即3b+2c<0,故③正确;
假设4n(an+b)≤a成立,
将b=2a代入,得:4n(an+2a)≤a,即4an2+8an≤a恒成立,
由图象可知a<0,
∴4n2+8n-1≤0,
解得:-$\frac{\sqrt{5}+2}{2}$≤n≤$\frac{\sqrt{5}-2}{2}$,故④错误;
综上,正确结论是②③,
故选:C.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
2.某大学为了解法学院1500名新生的身高情况,采用随机抽查的方式用300名新生的身高为样本进行统计,其中身高在170cm-175cm的有75人,那么估计法学院新生身高在170cm-175cm的人数约是( )
| A. | 300 | B. | 325 | C. | 375 | D. | 450 |
2.下面各整式能直接运用完全平方公式分解因式的是( )
| A. | x2-x+1 | B. | x2+2x-1 | C. | -2x+x2+1 | D. | 2x-x2+1 |
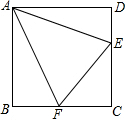 已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.
已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.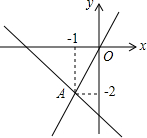 如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.
如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.