题目内容
11.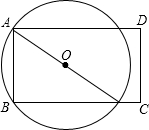 已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.
已知,如图,在矩形ABCD中,AB=6,BC=8,P点是线段BC上的任一动点,过点A、B、P作⊙O,设⊙O的半径为r,当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.
分析 如图1,当⊙O与CD相切于E时,根据切割线定理求得PB=$\frac{55}{8}$,根据勾股定理得到AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\frac{73}{8}$,求得r=$\frac{73}{16}$,如图2,当矩形ABCD内接于⊙O时,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,求得r=5,于是得到结论.
解答  解:如图1,当⊙O与CD相切于E时,
解:如图1,当⊙O与CD相切于E时,
则CE=$\frac{1}{2}$CD=$\frac{1}{2}$AB=3,
设PB=x,
∴CE2=CP•BC,即32=(8-x)×8,
∴x=$\frac{55}{8}$,
∴PB=$\frac{55}{8}$,
∴AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\frac{73}{8}$,
∴r=$\frac{73}{16}$,
如图2,当矩形ABCD内接于⊙O时,
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∴r=5,
∴当⊙O与线段CD有且只有两个交点时,半径r的取值范围是$\frac{73}{16}$<r≤5.
故答案为:$\frac{73}{16}$<r≤5.
点评 本题考查了直线与圆的位置关系:判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d:直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了相似三角形的判定与性质.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.某大学为了解法学院1500名新生的身高情况,采用随机抽查的方式用300名新生的身高为样本进行统计,其中身高在170cm-175cm的有75人,那么估计法学院新生身高在170cm-175cm的人数约是( )
| A. | 300 | B. | 325 | C. | 375 | D. | 450 |
6.抛物线y=-$\frac{1}{2}$(x+1)2-2的顶点坐标是( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (1,2) |
16.下列调查中,适合用普查(全面调查)方式的是( )
| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解一批灯泡的使用寿命 | |
| C. | 了解江苏卫视“非诚勿扰”节目的收视率 | |
| D. | 了解某班学生“100米跑”的成绩 |
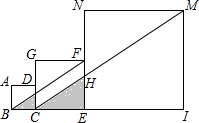 正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$.
正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$.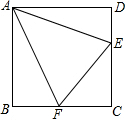 已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.
已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.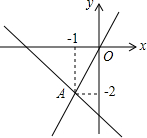 如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.
如图,在平面直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象交于点A,则关于x的不等式k1x+b<k2x的解集为x>-1.