题目内容
5．在Rt△ABC中，∠C=90°，tanA=2，则cosB=$\frac{2\sqrt{5}}{5}$．分析 根据正切函数，可用AC表示BC，根据勾股定理，可得AC表示AB，再根据余弦定理，可得答案．
解答 解：在Rt△ABC中，∠C=90°，得
AB为斜边．
由tanA=$\frac{BC}{AC}$=2，得
BC=2AC．
在Rt△ABC中，∠C=90°，由勾股定理，得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$AC．
cosB=$\frac{BC}{AB}$=$\frac{2AC}{\sqrt{5}AC}$=$\frac{2\sqrt{5}}{5}$，
故答案为：$\frac{2\sqrt{5}}{5}$．
点评 本题考查了互为余角三角函数关系，利用正切函数、勾股定理得出AC表示BC，AC表示AB是解题关键．
练习册系列答案
相关题目
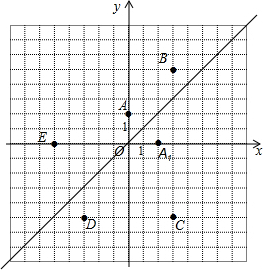如图，在平面直角坐标系中，函数y=x的图象是第一、三象限的角平分线．
已知常数a（a是整数）满足下面两个要求：
已知图1、图2、图3都是4×5的方格纸，其中每个小正方形的边长均为1cm，每个小正方形的顶点称为格点．