题目内容
20.已知二次函数y=(x-1)(mx-2)(m是常数,m≠0,且m≠2)(1)求函数的图象与x轴的交点A、B,与y轴交点C的坐标;
(2)若函数的图象与x、y轴的交点恰好构成直角三角形的三个顶点,求m的值.
分析 (1)根据抛物线与x轴的交点问题,通过解方程(x-1)(mx-2)=0即可得到点A、B的坐标,然后计算自变量为0时的函数值即可得到C点坐标;
(2)由于△ACB为直角三角形,利用点A和点C的坐标特征可判断点A与点B在y轴两侧,且∠ACB=90°,接着证明Rt△OBC∽Rt△OCA,利用相似比可得到2:1=-$\frac{2}{m}$:2,然后根据比例性质可求出m的值.
解答 解:(1)当y=0时,(x-1)(mx-2)=0,解得x1=1,x2=$\frac{2}{m}$,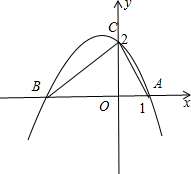
所以函数的图象与x轴的交点A、B的坐标为(1,0),($\frac{2}{m}$,0),
当x=0时,y=(x-1)(mx-2)=2,则C点坐标为(0,2);
(2)∵△ACB为直角三角形,
∴点A与点B在y轴两侧,∠ACB=90°,设A(1,0),B($\frac{2}{m}$,0),
∵∠OCB+∠OBC=90°,
而∠OCB+∠OCA=90°,
∴∠OBC=∠OCA,
∴Rt△OBC∽Rt△OCA,
∴OC:OA=OB:OC,即2:1=-$\frac{2}{m}$:2,
∴m=-$\frac{1}{2}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.证明Rt△OBC∽Rt△OCA,利用相似比得到关于m的方程是解决此题的根据.

练习册系列答案
相关题目
15.已知(-3,y1),(-15,y2),(2,y3)在反比例函数y=-$\frac{a^2}{x}$上,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
2.分式$\frac{3}{2a}$,$\frac{a}{3b}$,$\frac{1}{{6{c^2}}}$的最简公分母是( )
| A. | 6abc | B. | 6abc2 | C. | 12abc2 | D. | 36abc2 |

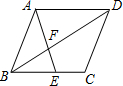 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{BC}=\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{BC}=\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$.