题目内容
9.如图,在平面直角坐标系中,A、B两点的坐标分别为(-3,4)、(-6,0).(1)求证:△ABO是等腰三角形;
(2)过点B作直线l,在直线l上取一点C,使AC∥x轴,且AC=AB.
①若直线l与边AO交于E点,求直线l的相应函数关系式及点E的坐标;
②设∠AOB=α,∠ACB=β,直接写出α与β的关系.
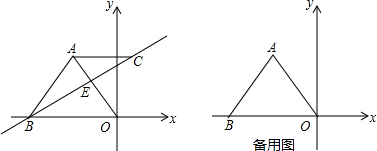
分析 (1)过A点作AH垂直OB于H点,根据A、B两点的坐标可得出BH=OH=3,再由勾股定理可得出AB=OA,由此可得出结论;
(2)①利用待定系数法求出直线l与OA的解析式,进而可得出E点坐标;
②分点C在点A的右边与左边两种情况进行讨论.
解答  解:(1)如图1,过A点作AH垂直OB于H点,
解:(1)如图1,过A点作AH垂直OB于H点,
∵A、B两点的坐标分别为(-3,4)、(-6,0).
∴BH=OH=3,AH=4,
∴AB=OA=5,
∴△ABO是等腰三形;
(2)①∵AC∥x轴且AC=AB.
∴C点坐标为(2,4);
设直线l的解析式为y=kx+b,把(-6,0),(2,4)代入得:$\left\{\begin{array}{l}-6k+b=0\\ 2k+b=4\end{array}\right.$
解得$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=3\end{array}\right.$,
∴设直线l的解析式为y=$\frac{1}{2}$x+3,
边AO所在直线的角析式为y=mx,把(-3,4)代入得:4=-3m,解得m=-$\frac{4}{3}$,
∴边AO所在直线的角析式为y=-$\frac{4}{3}$x,
联立$\left\{\begin{array}{l}y=\frac{1}{2}x+3\\ y=-\frac{4}{3}x\end{array}\right.$,解得$\left\{\begin{array}{l}x=-\frac{18}{11}\\ y=\frac{24}{11}\end{array}\right.$
∴E($-\frac{18}{11}$,$\frac{24}{11}$);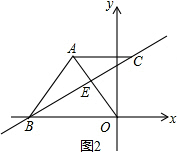
②当点C在点A的右边时,如图2所示,
∵AC∥x轴,
∴∠β=∠OBC.
∵AC=AB,
∴∠β=∠ABC,
∴α=2β;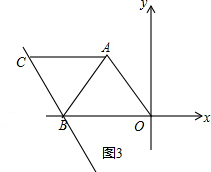 当点C在点A的左边时,如图3所示.
当点C在点A的左边时,如图3所示.
∵AC=AB,
∴∠ACB=∠ABC=β,
∴∠BAC=180°-2β.
∵AC∥OB,
∴∠ABO=∠BAC,
∴α=180°-2β.
综上所述,α与β的关系是α=2β或α=180°-2β.
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点及用待定系数法求一次函数的解析式等知识,在解答(2)时要注意进行分类讨论,不要漏解.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
| A. | 想了解某种饮料中含色素的情况,宜采用抽样调查 | |
| B. | 某中学“学生艺术节”元旦汇演活动时下雨是必然事件 | |
| C. | 数据3,1,1,2,2的中位数是1 | |
| D. | 一组数据的波动越大,方差越小 |
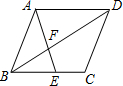 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{BC}=\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{BC}=\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$.