题目内容
13. 已知常数a(a是整数)满足下面两个要求:
已知常数a(a是整数)满足下面两个要求:①关于x的一元二次方程ax2+3x-1=0有两个不相等的实数根;
②反比例函数$y=\frac{2a+2}{x}$的图象在二,四象限.
(1)求a的值;
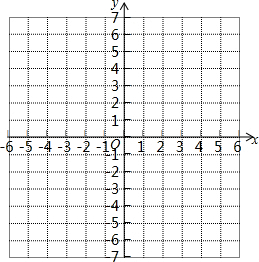
(2)在所给直角坐标系中用描点法画出$y=\frac{2a+2}{x}$的图象,并根据图象写出:
当x>4时,y的取值范围是-$\frac{1}{2}$<y<0;
当y<1时,x的取值范围是x<-2或x>0.
分析 (1)先根据关于x的一元二次方程ax2+3x-1=0有两个不相等的实数根求出a的取值范围,再由反比例函数$y=\frac{2a+2}{x}$的图象在二,四象限得出a的取值范围,由a为整数即可得出a的值;
(2)根据a的值得出反比例函数解析式,画出函数图象,由函数图象即可得出结论.
解答 解:(1)∵方程有两个不相等的实数根,
∴△=9+4a>0,得a>-$\frac{9}{4}$且a≠0;
∵反比例函数图象在二,四象限,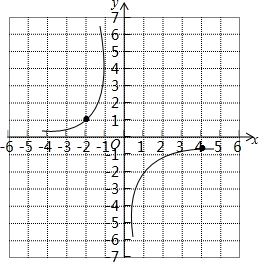
∴2a+2<0,得a<-1,
∴-$\frac{9}{4}$<a<-1.
∵a是整数,
∴a=-2;
(2)∵a=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$,
其函数图象如图所示;
当x>4时,y的取值范围-$\frac{1}{2}$<y<0;
当y<1时,x的取值范围是 x<-2或x>0.
故答案为:-$\frac{1}{2}$<y<0,x<-2或x>0.
点评 本题考查的是反比例函数的性质,根据题意画出函数图象,利用函数图象求出不等式的解集是解答此题的关键.

练习册系列答案
相关题目
3.一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同,红球、黄球、黑球的个数之比为5:3:1,则从布袋里任意摸出一个球是黄球的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{3}{8}$ |
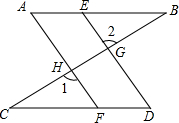 已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,∠A=∠D,∠1=∠2,∠B=30°,求∠C.
已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,∠A=∠D,∠1=∠2,∠B=30°,求∠C.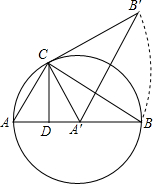 如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π.
如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π.