题目内容
8．不等式2x-1≤4的最大整数解是（ ）| A． | 0 | B． | 1 | C． | $\frac{5}{2}$ | D． | 2 |
分析 解不等式求得x的范围，再该范围内可得其最大整数解．
解答 解：移项、合并，得：2x≤5，
系数化为1，得：x≤2.5，
∴不等式的最大整数解为2，
故选：D．
点评 本题主要考查解不等式的能力，解决此类问题的关键在于正确解得不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件进而求得不等式的整数解．可以借助数轴进行数形结合，得到需要的值，进而非常容易的解决问题．
练习册系列答案
阅读快车系列答案
相关题目
19．已知一次函数y=-x+b，过点（-8，-2），那么一次函数的解析式为（ ）
| A． | y=-x-2 | B． | y=-x-6 | C． | y=-x-10 | D． | y=-x-1 |
16．
如图，将一条两边沿互相平行的纸袋按如图所示折叠，已知∠1=40°，则∠α的度数（ ）
如图，将一条两边沿互相平行的纸袋按如图所示折叠，已知∠1=40°，则∠α的度数（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
3．命题：“关于x的一元二次方程x2+bx+1=0，当b＜0时，必有实数根”；能说明这个命题是假命题的一个反例可以是（ ）
| A． | b=-1 | B． | b=-2 | C． | b=-3 | D． | b=-4 |
13．以下列各组数为三角形的三边，能构成直角三角形的是（ ）
| A． | 4，5，6 | B． | 1，1，$\sqrt{2}$ | C． | 6，8，11 | D． | 5，12，23 |
20．$\sqrt{3}tan（α+2{0°}）=1$，锐角α的度数应是（ ）
| A． | 40° | B． | 30° | C． | 20° | D． | 10° |
17．
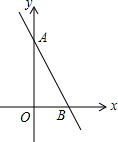如图，若一次函数y=-2x+b的图象交y轴于点A（0，3），则不等式-2x+b＞0的解集为（ ）
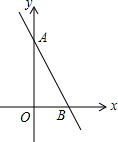如图，若一次函数y=-2x+b的图象交y轴于点A（0，3），则不等式-2x+b＞0的解集为（ ）| A． | x＞$\frac{3}{2}$ | B． | x＞3 | C． | x＜$\frac{3}{2}$ | D． | x＜3 |
18．下列计算正确的是（ ）
| A． | x2+x5=x7 | B． | x5-x2=3x | C． | x2•x5=x10 | D． | x5÷x2=x3 |