题目内容
9.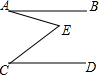 如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )
如图,AB∥CD,则∠BAE,∠AEC,∠ECD三个角之间的关系为( )| A. | ∠BAE=∠AEC+∠ECD | B. | ∠BAE=∠AEC-∠ECD | C. | ∠BAE=∠ECD-∠AEC | D. | 不能确定 |
分析 过E作EF∥AB,可得∠A=∠AEF,利用平行于同一条直线的两直线平行得到EF与CD平行,再得到一对内错角相等,进而得出答案.
解答  解:如图,过E作EF∥AB,可得∠A=∠AEF,
解:如图,过E作EF∥AB,可得∠A=∠AEF,
∵AB∥CD,
∴EF∥CD,
∴∠FEC=∠C,
∵∠AEC=∠AEF+∠FEC,
∴∠A=∠AEC-∠C,
即∠BAE=∠AEC-∠ECD.
故选:B.
点评 此题考查了平行线的性质,熟练掌握平行线的性质作出辅助线是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.已知一次函数y=-x+b,过点(-8,-2),那么一次函数的解析式为( )
| A. | y=-x-2 | B. | y=-x-6 | C. | y=-x-10 | D. | y=-x-1 |
20.$\sqrt{3}tan(α+2{0°})=1$,锐角α的度数应是( )
| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
17.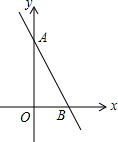 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
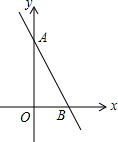 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )| A. | x>$\frac{3}{2}$ | B. | x>3 | C. | x<$\frac{3}{2}$ | D. | x<3 |
4.若五个正整数的中位数是3,且唯一的众数是7,则这五个数的平均数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
14.平面直角坐标中,点M(0,-3)在( )
| A. | 第二象限 | B. | 第四象限 | C. | x轴上 | D. | y轴上 |
1.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
| A. | 7,24,25 | B. | 3,4,$\frac{14}{3}$ | C. | 3,4,5 | D. | 15,8,17 |
18.下列计算正确的是( )
| A. | x2+x5=x7 | B. | x5-x2=3x | C. | x2•x5=x10 | D. | x5÷x2=x3 |
10.下列各式中去括号正确的是( )
| A. | a2-4(-a+1)=a2-4a-4 | B. | -(mn-1)+(m-n)=-mn-1+m-n | ||
| C. | 5x-(2x-1)-x2=5x-2x+1-x2 | D. | x2-2(2x-y+2)=x2-4x+y-2 |