题目内容
10.下列命题中,假命题是( )| A. | 有两角和其中一角的对边对应相等的两个三角形全等 | |
| B. | 面积相等的两个三角形全等 | |
| C. | 有一边相等的两个等边三角形全等 | |
| D. | 三边对应相等的两个三角形全等 |
分析 利用全等三角形的判定方法分别对每个选项进行判断后即可确定正确的选项.
解答 解:A、有两角和其中一角的对边对应相等的两个三角形全等,正确,是真命题;
B、面积相等的三角形不一定全等,故错误,是假命题;
C、有一边相等的两个等边三角形全等,正确,是真命题;
D、三边对应相等的两个三角形全等,正确,为真命题;
故选:B.
点评 本题考查了命题与定理的知识,解题的关键是掌握全等三角形的判定的几种方法,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一次函数y=2x+4与x轴交点的坐标为( )
| A. | (0,4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
15.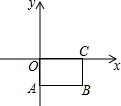 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )| A. | (4,2) | B. | (-2,4) | C. | (4,-2) | D. | (-4,2) |
2.下列命题中:
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
19.已知一次函数y=-x+b,过点(-8,-2),那么一次函数的解析式为( )
| A. | y=-x-2 | B. | y=-x-6 | C. | y=-x-10 | D. | y=-x-1 |
20.$\sqrt{3}tan(α+2{0°})=1$,锐角α的度数应是( )
| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
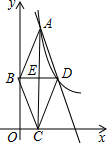 如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.
如图,点A是反比例函数y=$\frac{8}{x}$(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连结AB、BC、CD、DA.设点A的横坐标为m.