题目内容
5.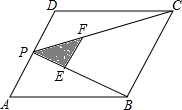 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )| A. | $\frac{10}{3}$ | B. | $\frac{9}{2}$ | C. | $\frac{13}{3}$ | D. | 4 |
分析 先作辅助线DH⊥AB于点D,然后根据特殊角的三角函数值可以求得DH的长度,从而可以求得平行四边形的面积,然后根据三角形的相似可以求得S1+S2+S3的值.
解答  解:作DH⊥AB于点H,如右图所示,
解:作DH⊥AB于点H,如右图所示,
∵AD=2,AB=2$\sqrt{3}$,∠A=60°,
∴DH=AD•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴S?ABCD=AB•DH=2$\sqrt{3}•\sqrt{3}$=6,
∴S2+S3=S△PBC=3,
又∵E、F分别是PB、PC(靠近点P)的三等分点,
∴$\frac{{S}_{△PEF}}{{S}_{△PBC}}=\frac{1}{9}$,
∴S△PEF=$\frac{1}{9}$×3=$\frac{1}{3}$,
即S1=$\frac{1}{3}$,
∴S1+S2+S3=$\frac{1}{3}$+3=$\frac{10}{3}$,
故选A.
点评 本题考查相似三角形的判定与性质、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,画出合适的辅助线,利用数形结合的思想解答问题.

练习册系列答案
相关题目
15.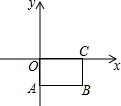 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )| A. | (4,2) | B. | (-2,4) | C. | (4,-2) | D. | (-4,2) |
16. 如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
 如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
13.以下列各组数为三角形的三边,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,1,$\sqrt{2}$ | C. | 6,8,11 | D. | 5,12,23 |
20.$\sqrt{3}tan(α+2{0°})=1$,锐角α的度数应是( )
| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
10.五一小长假虽只有三天,可美丽竹乡安吉的旅游市场却“火”到不行.记者从安吉县旅游部门获悉,2016年“五一”期间,全县共接待游客64.8万人次,同比增长20.7%.请将64.8万用科学记数法表示( )
| A. | 64.8×104 | B. | 6.48×105 | C. | 0.648×106 | D. | 6.48×106 |
17.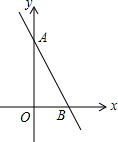 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
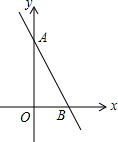 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )| A. | x>$\frac{3}{2}$ | B. | x>3 | C. | x<$\frac{3}{2}$ | D. | x<3 |
14.平面直角坐标中,点M(0,-3)在( )
| A. | 第二象限 | B. | 第四象限 | C. | x轴上 | D. | y轴上 |
6.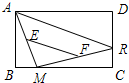 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )| A. | 变短 | B. | 变长 | C. | 不变 | D. | 无法确定 |