题目内容
19.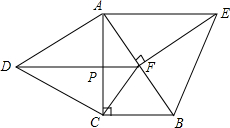 如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.
如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形;
(3)直接写出图中所有等腰三角形.
分析 (1)由已知条件可证得△ACB≌△EFB,从而得到AC=EF;
(2)由上题结论结合等边△ACD可证得AD=EF,再利用角度证出AD∥EF就可以证出四边形ADFE是平行四边形;
(3)结合直角三角形斜边上的中线等于斜边的一半性质,再结合等边三角形就可以得出所有的等腰三角形.
解答 解:(1)∵∠BAC=30° EF⊥AB
∴AB=2BC∠ABC=60°
∵等边△ABE
∴AB=BE∠FBE=60°
∵EF⊥AB
∴BE=2BF
∴BC=BF
在△ACB与△EFB中,
$\left\{\begin{array}{l}{AB=EB}\\{∠ABC=∠EBF}\\{BC=BF}\end{array}\right.$,
∴△ACB≌△EFB(SAS)
∴AC=EF
(2)∵等边△ACD
∴∠DAP=60°AD=AC
∴∠DAF=90°AD=EF
∵EF⊥AB
∴AD∥EF
∴四边形ADFE是平行四边形
(3)由(1)可知F为AB中点
∵AC⊥BC
∴AF=FC=FB
∴图中所有的等腰三角形为△ACD、△ABE、△ACF、△FCB
点评 本题考查平行四边形、直角三角形及等腰三角形性质,解题的关键是要灵活运用直角三角形30°所对的边等于斜边的一半,找出边之间的等量关系.

练习册系列答案
相关题目
3.下列等式一定成立的是( )
| A. | a2+a3=a5 | B. | (a+b)2=a2+b2 | ||
| C. | (-a+b)(-a-b)=-a2-b2 | D. | (x-a)(x-b)=x2-(a+b)x+ab |
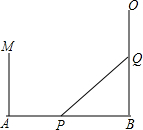 如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等. 如图,等腰直角三角形的斜边长AB=8,一直线l绕顶点B任意旋转,过A向l作垂线,垂足为H,则线段CH长的取值范围是0≤CH≤8.
如图,等腰直角三角形的斜边长AB=8,一直线l绕顶点B任意旋转,过A向l作垂线,垂足为H,则线段CH长的取值范围是0≤CH≤8.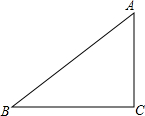 尺规作图:已知△ABC,如图.
尺规作图:已知△ABC,如图.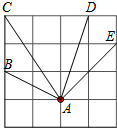 如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD.
如图,在4×4的网格图中,小正方形的边长为1,则图中用字母表示的四条线段中长度为$\sqrt{10}$的线段是AD. 如图:∠1与∠2是内错角吗是(是或不是)
如图:∠1与∠2是内错角吗是(是或不是)