题目内容
3.下列等式一定成立的是( )| A. | a2+a3=a5 | B. | (a+b)2=a2+b2 | ||
| C. | (-a+b)(-a-b)=-a2-b2 | D. | (x-a)(x-b)=x2-(a+b)x+ab |
分析 由合并同类项得出A不成立;由完全平方公式得出B不成立;由平方差公式得出C不成立;由多项式乘多项式的法则得出D成立.
解答 解:A、a2与a3不是同类项,不能合并;
∴选项A不成立;
B、∵(a+b)2=a2+2ab+b2,
∴选项B不成立;
C、∵(-a+b)(-a-b)=(-a)2-b2=a2-b2,
∴选项C不成立;
D、∵(x-a)(x-b)=x2-(a+b)x+ab,
∴选项D成立;
故选D.
点评 本题考查了平方差公式、合并同类项、多项式与多项式相乘的法则、完全平方公式;熟练掌握有关公式和法则是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列计算正确的是( )
| A. | -($\sqrt{6}$)2=-6 | B. | ($\sqrt{3}$)2=9 | C. | ($\sqrt{16}$)2=±16 | D. | -(-$\sqrt{\frac{16}{25}}$)2=$\frac{16}{25}$ |
8.下列各式中一定是二次根式的是( )
| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\root{3}{{\frac{a}{b}}}$ |
15.下列说法正确的是( )
| A. | a,-6,ab+c,$\frac{2x-1}{3}$都是整式 | B. | $\frac{x+y}{2}$和$\frac{xy}{2}$都是单项式 | ||
| C. | $\frac{y+1}{y}$和x2+xy+y2都是多项式 | D. | 3x-1的项是3x和1 |
13.下列各式表示正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $±\sqrt{25}=5$ | C. | $\root{3}{-27}$=-3 | D. | $±\sqrt{(-5)^{2}}=-5$ |
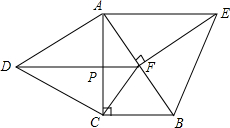 如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.
如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.