题目内容
14.已知a,b为正整数,于x的方程x2-2ax+b=0的两个实数根为x1,x2,关于y的方程y2+2ay+b=0的两个实数根为y1,y2,求x1y1-x2y2的最小值.分析 公式法分别表示两方程的解为a±$\sqrt{{a}^{2}-b}$、-a±$\sqrt{{a}^{2}-b}$,令t=$\sqrt{{a}^{2}-b}$后分以下4种情况:①x1=a+t,x2=a-t,y1=-a+t,y2=-a-t;②x1=a-t,x2=a+t,y1=-a-t,y2=-a+t;③x1=a-t,x2=a+t,y1=-a-t,y2=-a-t;④x1=a+t,x2=a-t,y1=-a-t,y2=-a+t;分别表示出x1y1-x2y2,求出相应最小值,综合可得.
解答 解:关于x方程x2-2ax+b=0的两个实数根为$\frac{2a±\sqrt{4{a}^{2}-4b}}{2}$=a±$\sqrt{{a}^{2}-b}$,
关于y的方程y2+2ay+b=0的两个实数根为$\frac{-2a±\sqrt{4{a}^{2}-4b}}{2}$=-a±$\sqrt{{a}^{2}-b}$,
设t=$\sqrt{{a}^{2}-b}$,
①当x1=a+t,x2=a-t,y1=-a+t,y2=-a-t时,
x1y1-x2y2=0;
②当x1=a-t,x2=a+t,y1=-a-t,y2=-a+t时,
x1y1-x2y2=0;
③当x1=a-t,x2=a+t,y1=-a-t,y2=-a-t时,
x1y1-x2y2=4at,
∵方程有实数根,
∴t≥0,
∴x1y1-x2y2=4at≥0,此时其最小值为0;
④当x1=a+t,x2=a-t,y1=-a-t,y2=-a+t时,
x1y1-x2y2=-4at,
∵t≥0,
∴x1y1-x2y2=-4at≤0,即x1y1-x2y2无最小值,
综上,x1y1-x2y2的最小值为0.
点评 本题主要考查一元二次方程的根与系数的关系,表示出各方程的根并通过换元简化各根式,分类讨论求x1y1-x2y2的最值是关键.

 名校课堂系列答案
名校课堂系列答案 如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )
如图,直线l1∥l2,∠A=124°,∠B=86°,则∠1+∠2=( )| A. | 30° | B. | 35° | C. | 36° | D. | 40° |
| A. | m>-1.5 | B. | m<-1.5 | C. | m>1.5 | D. | m<1.5 |
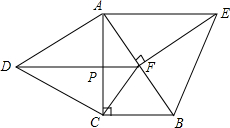 如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF.
如图,分别以Rt△ABC的直角边AC及斜边AB向形外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF、CF. 已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).
已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).