题目内容

1．解分式方程：$\frac{x}{x+2}$-1=$\frac{8}{{x}^{2}-4}$．

分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答 解：去分母得：x2-2x-x2+4=8，
解得：x=-2，
检验：将x=-2代入最简公分母（x+2）（x-2）=0，
则x=-2是原方程的增根，原方程无解．

点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

练习册系列答案
相关题目
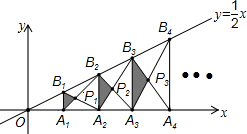11．如图，已知A1，A2，A3，…，An，An+1是x轴上的点，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1，A2，A3，…，An，An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1，B2，B3，…，Bn，Bn+1，连接A1B2，B1A2，A2B3，B2A3，…，AnBn+1，BnAn+1，依次相交于点P1，P2，P3，…，Pn，△A1B1P1，△A2B2P2，…，△AnBnPn的面积依次记为S1，S2，S3，…，Sn，则Sn=$\frac{{n}^{2}}{8n+4}$（请用含n的代数式表示）．
12．无理数a满足：2＜a＜3，那么a可能是（　　）
A．$\sqrt{10}$B．$\sqrt{6}$C．2.5D．$\frac{20}{7}$
9．已知点A（0，-4），B（8，0）和C（a，a），以线段AB的中点为圆心的圆过点C，则这个圆的半径的最小值等于3$\sqrt{2}$．
16．在0，-2，-1，3这四个数中，最小的数是（　　）
A．3B．-1C．0D．-2
3．已知△ABC，∠ACB=90°，点D（0，-3），M（4，-3）．
（1）如图1，若点C与点O重合，且A（-3，a），B（3，b），a+b-8=0，求△ACB的面积；
（2）如图2，若∠AOG=50°，求∠CEF的度数；
（3）如图3，旋转△ABC，使∠C的顶点C在直线DM与x轴之间，N为AC上一点，E为BC与DM的交点∠NEC+∠CEF=180°，下列两个结论：①∠NEF-∠AOG为定值；②$\frac{∠NEF}{∠AOG}$为定值，其中只有一个是正确的，请你判断出正确的结论，并求其值．
10．已知，如图，△ABC为等边三角形，∠BDC=60°，连接AD．
（1）如图1，若AD=CD，求证：BD=2CD；
（2）如图2，若AD=mCD，求$\frac{BD}{CD}$的值．
7．如图，所有小正方形的边长都为1，A、B、C都在格点上．
（1）过点C画直线AB的平行线（仅利用所给方格纸和直尺作图，下同）；
（2）过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H．
（3）线段AG的长度是点A到直线BC的距离；线段AH的长度是点H到直线AB的距离．
（4）线段AG、AH的大小关系为：AG=$\frac{\sqrt{2}}{2}$AH．理由：△AGH是等腰直角三角形，．
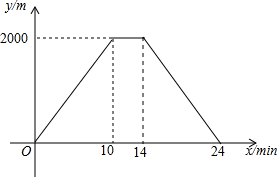8．小明骑自行车从甲地到乙地，到达乙地后，休息了一段时间，然后原路返回，停在甲地．整个过程保持匀速前进，设小明出发x（min）后，到达距离甲地y（m）的地方，图中的折线表示的是y与x之间的函数关系．
（1）求小明从乙地返回甲地过程中，y与x之间的函数关系式；
（2）在小明从甲地出发的同时，小红从乙地步行至甲地，保持80m/min的速度不变，到甲地停止．请在同一坐标系中画出小红离甲地的距离y与x之间的函数图象（标注图象与坐标轴交点的坐标）；
（3）小明和小红出发14分钟以后，他们何时相距40米？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网